题目内容
已知F1,F2分别是双曲线
-
=l(a>0,b>0)的左、右焦点,P为双曲线上的一点,若∠F1PF2=90°,且△F1PF2的三边长成等差数列.又一椭圆的中心在原点,焦点在x轴上,短轴的一个端点到其右焦点的距离为
,双曲线与该椭圆离心率之积为
.
(1)求椭圆的方程;
(2)设直线l与椭圆交于A,B两点,坐标原点O到直线l的距离为
,求△AOB面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
5
| ||
| 3 |
(1)求椭圆的方程;
(2)设直线l与椭圆交于A,B两点,坐标原点O到直线l的距离为
| ||
| 2 |
考点:双曲线的简单性质
专题:计算题,等差数列与等比数列,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)设P为双曲线的右支上的点,运用双曲线的定义和等差数列的性质,以及勾股定理,得到a,c的关系,再由离心率公式得到双曲线的离心率为5,进而得到椭圆的离心率,由条件可得a=
,再由离心率公式,即可得到椭圆的方程;
(2)设A(x1,y1),B(x2,y2).分当AB⊥x轴时与AB与x轴不垂直时求出|AB|.当AB与x轴不垂直时,设直线AB的方程为y=kx+m,由坐标原点O到直线l的距离为
可得
=
,化为m2=
(k2+1),同时将直线方程与椭圆方程联立得到根与系数的关系,利用弦长公式即可得出|AB|,再由基本不等式求得|AB|的最大值,运用三角形的面积公式,即可得到面积的最大值.
| 3 |
(2)设A(x1,y1),B(x2,y2).分当AB⊥x轴时与AB与x轴不垂直时求出|AB|.当AB与x轴不垂直时,设直线AB的方程为y=kx+m,由坐标原点O到直线l的距离为
| ||
| 2 |
| |m| | ||
|
| ||
| 2 |
| 3 |
| 4 |
解答:
解:(1)设P为双曲线的右支上的点,
|PF1|-|PF2|=2a,①
又PF2,PF1,F1F2成等差数列,则有|PF2|+|F1F2|=2|PF1|,
即2|PF1|-|PF2|=|F1F2|=2c,②
由①②解得,|PF1|=2(c-a),|PF2|=2(c-2a),
由于∠F1PF2=90°,则|PF1|2+|PF2|2=|F1F2|2,
则4(c-a)2+4(c-2a)2=4c2,
化简得,c2-6ac+5a2=0,
解得,c=5a,即有双曲线的离心率为5,
则由双曲线与该椭圆离心率之积为
,
即有椭圆的离心率为
,
设椭圆的方程为
+
=1(m>n>0),
由于椭圆短轴的一个端点到其右焦点的距离为
,即有m=
,
则
=
,解得,n=1,
则有椭圆方程为
+y2=1;
(2)设A(x1,y1),B(x2,y2),
①当AB⊥x轴时,∵坐标原点O到直线l的距离为
,
∴可取A(
,y1),代入椭圆得
+y12=1,解得y1=±
.
∴|AB|=
;
②当AB与x轴不垂直时,设直线AB的方程为y=kx+m,
由坐标原点O到直线l的距离为
,可得
=
,化为m2=
(k2+1).
把y=kx+m代入椭圆方程,消去y得到(3k2+1)x2+6kmx+3m2-3=0,
∴x1+x2=-
,x1x2=
.
∴|AB|2=(1+k2)[(x1+x2)2-4x1x2]
=(1+k2)[(-
)2-4•
]
=
=
=3+
.
当k≠0时,|AB|2=3+
≤3+
=4,
当且仅当k2=
时取等号,此时|AB|=2.
当k=0时,|AB|=
.
综上可知:|AB|max=2.△OAB的面积最大值为=
×2×
=
.
|PF1|-|PF2|=2a,①
又PF2,PF1,F1F2成等差数列,则有|PF2|+|F1F2|=2|PF1|,
即2|PF1|-|PF2|=|F1F2|=2c,②
由①②解得,|PF1|=2(c-a),|PF2|=2(c-2a),
由于∠F1PF2=90°,则|PF1|2+|PF2|2=|F1F2|2,
则4(c-a)2+4(c-2a)2=4c2,
化简得,c2-6ac+5a2=0,
解得,c=5a,即有双曲线的离心率为5,
则由双曲线与该椭圆离心率之积为
5
| ||
| 3 |
即有椭圆的离心率为
| ||
| 3 |
设椭圆的方程为
| x2 |
| m2 |
| y2 |
| n2 |
由于椭圆短轴的一个端点到其右焦点的距离为
| 3 |
| 3 |
则
| m2-n2 |
| 2 |
则有椭圆方程为
| x2 |
| 3 |
(2)设A(x1,y1),B(x2,y2),
①当AB⊥x轴时,∵坐标原点O到直线l的距离为
| ||
| 2 |
∴可取A(
| ||
| 2 |
| ||
| 3 |
| ||
| 2 |
∴|AB|=
| 3 |
②当AB与x轴不垂直时,设直线AB的方程为y=kx+m,
由坐标原点O到直线l的距离为
| ||
| 2 |
| |m| | ||
|
| ||
| 2 |
| 3 |
| 4 |
把y=kx+m代入椭圆方程,消去y得到(3k2+1)x2+6kmx+3m2-3=0,
∴x1+x2=-
| 6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
∴|AB|2=(1+k2)[(x1+x2)2-4x1x2]
=(1+k2)[(-
| 6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
=
| 12(1+k2)(1+3k2-m2) |
| (1+3k2)2 |
| 3(1+k2)(9k2+1) |
| (1+3k2)2 |
| 12k2 |
| 9k4+6k2+1 |
当k≠0时,|AB|2=3+
| 12 | ||
9k2+
|
| 12 |
| 2×3+6 |
当且仅当k2=
| 1 |
| 3 |
当k=0时,|AB|=
| 3 |
综上可知:|AB|max=2.△OAB的面积最大值为=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:本题考查椭圆和双曲线的定义和性质,熟练掌握直线与椭圆相交问题转化为方程联立得到根与系数的关系、弦长问题、三角形的面积、点到直线的距离公式、分类讨论的思想方法的方法等是解题的关键.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
已知θ是第一象限角,则方程x2+y2sinθ=1表示的图形是( )
| A、圆 | B、椭圆 |
| C、双曲线 | D、圆或椭圆 |
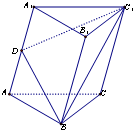 如图,三棱柱ABC-A1B1C1中,D是棱AA1的中点,平面BDC1分此棱柱为上下两部分,则这上下两部分体积的比为( )
如图,三棱柱ABC-A1B1C1中,D是棱AA1的中点,平面BDC1分此棱柱为上下两部分,则这上下两部分体积的比为( )| A、2:3 | B、1:1 |
| C、3:2 | D、3:4 |