题目内容
已知函数f(x)=3-2log2x,g(x)=log2x
(1)如果x∈[1,2],求函数h(x)=[f(x)+1]g(x)的值域;
(2)求函数M(x)=
的最大值.
(3)如果对任意x∈[1,2],不等式f(x2)f(
)>k•g(x)恒成立,求实数k的取值范围.
(1)如果x∈[1,2],求函数h(x)=[f(x)+1]g(x)的值域;
(2)求函数M(x)=
| f(x)+g(x)-|f(x)-g(x)| |
| 2 |
(3)如果对任意x∈[1,2],不等式f(x2)f(
| x |
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)令t=log2x,则h(x)=-2(t-1)2+2.由x∈[1,2],可得t∈[0,1],再利用二次函数的性质求得h(x)的值域.
(2)根据函数M(x)=
,f(x)-g(x)=3(1-log2x),分类讨论求得M(x)的最大值.
(3)由题意可得(3-4log2x)(3-log2x)>klog2x,根据t∈[0,1],可得(3-4t)(3-t)>kt对一切t∈[0,1]恒成立.再分①当t=0和②当t∈[0,1]两种情况,求得k的取值范围.
(2)根据函数M(x)=
|
(3)由题意可得(3-4log2x)(3-log2x)>klog2x,根据t∈[0,1],可得(3-4t)(3-t)>kt对一切t∈[0,1]恒成立.再分①当t=0和②当t∈[0,1]两种情况,求得k的取值范围.
解答:
解:(1)令t=log2x,则f(x)=3-t,g(x)=t,
h(x)=(4-2log2x)•log2x=-2(t-1)2+2.
∵x∈[1,2],∴t∈[0,1],
故当t=1时,h(x)取得最大值为2,当t=2时,函数取得最小值为0,
∴h(x)的值域为[0,2].
(2)函数M(x)=
=
,
∵f(x)-g(x)=3(1-log2x),
∴当x∈(0,2]时,f(x)≥g(x) M(x)=log2x.
当x∈(2,+∞)时,f(x)<g(x) M(x)=3-2log2x.
即M(x)=
.
当0<x≤2时,M(x)最大值为1;当x>2时,M(x)<1.
综上:当x=2时,M(x)取到最大值为1.
(3)∵对任意x∈[1,2],不等式f(x2)f(
)>k•g(x)恒成立,
即(3-4log2x)(3-log2x)>klog2x,
∵x∈[1,2],∴t∈[0,1],∴(3-4t)(3-t)>kt对一切t∈[0,1]恒成立.
①当t=0时k∈R.
②当t∈[0,1],k<
+4t-15,∵h(t)=
+4t-15在(0,1]上是减函数,
∴h(t)min=-2,(t=1时),∴k<-2.
综述,k的取值范围为(-∞,-2).
h(x)=(4-2log2x)•log2x=-2(t-1)2+2.
∵x∈[1,2],∴t∈[0,1],
故当t=1时,h(x)取得最大值为2,当t=2时,函数取得最小值为0,
∴h(x)的值域为[0,2].
(2)函数M(x)=
| f(x)+g(x)-|f(x)-g(x)| |
| 2 |
|
∵f(x)-g(x)=3(1-log2x),
∴当x∈(0,2]时,f(x)≥g(x) M(x)=log2x.
当x∈(2,+∞)时,f(x)<g(x) M(x)=3-2log2x.
即M(x)=
|
当0<x≤2时,M(x)最大值为1;当x>2时,M(x)<1.
综上:当x=2时,M(x)取到最大值为1.
(3)∵对任意x∈[1,2],不等式f(x2)f(
| x |
即(3-4log2x)(3-log2x)>klog2x,
∵x∈[1,2],∴t∈[0,1],∴(3-4t)(3-t)>kt对一切t∈[0,1]恒成立.
①当t=0时k∈R.
②当t∈[0,1],k<
| 9 |
| t |
| 9 |
| t |
∴h(t)min=-2,(t=1时),∴k<-2.
综述,k的取值范围为(-∞,-2).
点评:本题主要考查对数函数的图象和性质综合应用,函数的恒成立问题,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若函数f(x)=x2+ax是偶函数,则实数a=( )
| A、-2 | B、-1 | C、0 | D、1 |
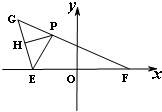 如图,在平面直角坐标系中,点E,F是x轴上的两个定点,|EO|=|OF|=
如图,在平面直角坐标系中,点E,F是x轴上的两个定点,|EO|=|OF|=