题目内容
已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在X轴上,离心率e=
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设椭圆E的右顶点为B,直线l过左焦点F1且垂直于X轴,交椭圆于M、N两点,求△BMN的面积.
| 1 |
| 2 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)设椭圆E的右顶点为B,直线l过左焦点F1且垂直于X轴,交椭圆于M、N两点,求△BMN的面积.
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用离心率e=
,可得b2=3c2,设椭圆方程为
+
=1把A(2,3)代入,即可求椭圆E的方程;
(Ⅱ)求出M,N的坐标,|BF1|=a+c=6,即可求△BMN的面积.
| 1 |
| 2 |
| x2 |
| 4c2 |
| y2 |
| 3c2 |
(Ⅱ)求出M,N的坐标,|BF1|=a+c=6,即可求△BMN的面积.
解答:
解:(Ⅰ)由e=
=
⇒a2=4c2,∴b2=3c2
于是可设椭圆方程为
+
=1把A(2,3)代入得c2=4
∴所求椭圆E的方程为
+
=1
(Ⅱ)由(Ⅰ)可知a=4,c=2,
∴左焦点F1(-2,0),B(4,0),|BF1|=a+c=6
把x=-2代入方程得M(-2,3)、N(-2,-3),
∴△BMN的面积=
|MN|•|BF1|=
×6×6=18.
| c |
| a |
| 1 |
| 2 |
于是可设椭圆方程为
| x2 |
| 4c2 |
| y2 |
| 3c2 |
∴所求椭圆E的方程为
| x2 |
| 16 |
| y2 |
| 12 |
(Ⅱ)由(Ⅰ)可知a=4,c=2,
∴左焦点F1(-2,0),B(4,0),|BF1|=a+c=6
把x=-2代入方程得M(-2,3)、N(-2,-3),
∴△BMN的面积=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查椭圆的方程与性质,考查三角形面积的计算,考查学生的计算能力,难度中等.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
抛物线y2=8x与双曲线
-
=1的一个焦点重合,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
| D、4 |
下面几个推理过程是演绎推理的是( )
| A、某同学第一次数学考试65分,第二次考试68分,由此预测其第三次考试71分 | ||
| B、根据圆的面积为S=πr2,推测球的体积为V=πr3 | ||
C、在数列{an}中,根据a1=1,an+1=
| ||
| D、因为平行四边形的对角线互相平分,而菱形是平行四边形,所以菱形的对角线互相平分 |
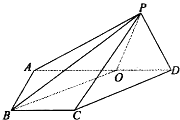 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.