题目内容
15.设D是△ABC所在平面内一点,$\overrightarrow{AB}$=2$\overrightarrow{DC}$,则( )| A. | $\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{AC}$-$\overrightarrow{AB}$ | B. | $\overrightarrow{BD}$=$\overrightarrow{AC}$-$\frac{1}{2}$$\overrightarrow{AB}$ | C. | $\overrightarrow{BD}$=$\frac{3}{2}$$\overrightarrow{AC}$-$\overrightarrow{AB}$ | D. | $\overrightarrow{BD}$=$\overrightarrow{AC}$-$\frac{3}{2}$$\overrightarrow{AB}$ |
分析 根据平面向量线性运算的几何意义用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{BD}$.
解答 解:$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$,$\overrightarrow{CD}=-\frac{1}{2}\overrightarrow{AB}$,
∴$\overrightarrow{BD}=\overrightarrow{BC}+\overrightarrow{CD}$=$\overrightarrow{AC}-\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AB}$=$\overrightarrow{AC}-\frac{3}{2}\overrightarrow{AB}$.
故选:D.
点评 本题考查了平面向量线性运算的几何意义,属于基础题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
6.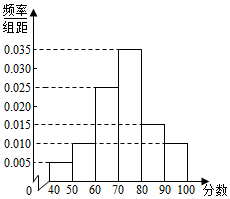 某中学对1000名学生的英语拓展水平测试成绩进行统计,得到样本频率分布直方图如图所示,现规定不低于80分为优秀,则优秀人数是( )
某中学对1000名学生的英语拓展水平测试成绩进行统计,得到样本频率分布直方图如图所示,现规定不低于80分为优秀,则优秀人数是( )
 某中学对1000名学生的英语拓展水平测试成绩进行统计,得到样本频率分布直方图如图所示,现规定不低于80分为优秀,则优秀人数是( )
某中学对1000名学生的英语拓展水平测试成绩进行统计,得到样本频率分布直方图如图所示,现规定不低于80分为优秀,则优秀人数是( )| A. | 250 | B. | 200 | C. | 150 | D. | 100 |
10.已知p:函数f(x)=(x-a)2在(-∞,-1)上是减函数,$q:?x>0,a≤\frac{{{x^2}+1}}{x}$恒成立,则¬p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.若2cos2α=sin($\frac{π}{4}$-α),且α∈($\frac{π}{2}$,π),则sin2α的值为( )
| A. | -$\frac{7}{8}$ | B. | -$\frac{\sqrt{15}}{8}$ | C. | 1 | D. | $\frac{\sqrt{15}}{8}$ |
4.已知i为虚数单位,复数z=1+2i,z与$\overline z$共轭,则$z\overline z$等于( )
| A. | 3 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 5 |
5.已知i为虚数单位,a为正实数,若|$\frac{a-i}{i}$|=2,则a=( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
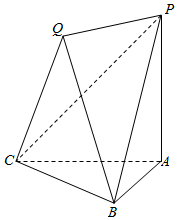 如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.
如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.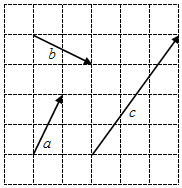 如图,网格纸上小正方形的边长为1,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),则x+y=$\frac{13}{5}$.
如图,网格纸上小正方形的边长为1,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),则x+y=$\frac{13}{5}$.