题目内容
10.已知p:函数f(x)=(x-a)2在(-∞,-1)上是减函数,$q:?x>0,a≤\frac{{{x^2}+1}}{x}$恒成立,则¬p是q的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 对于命题p:利用二次函数的单调性可得:-1≤a,¬p:a<-1.对于命题q:由于x>0,利用基本不等式的性质可得:$\frac{{x}^{2}+1}{x}$=x+$\frac{1}{x}$≥2,即可得出结论.
解答 解:p:函数f(x)=(x-a)2在(-∞,-1)上是减函数,∴-1≤a,∴¬p:a<-1.
q:∵x>0,∴$\frac{{x}^{2}+1}{x}$=x+$\frac{1}{x}$≥$2\sqrt{x•\frac{1}{x}}$=2,当且仅当x=1时取等号,∴a≤2.
则¬p是q的充分不必要条件.
故选:A.
点评 本题考查了不等式的解法、函数的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.“xy≠0”是“x≠0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.已知i为虚数单位,则z=$\frac{i}{1-2i}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.设D是△ABC所在平面内一点,$\overrightarrow{AB}$=2$\overrightarrow{DC}$,则( )
| A. | $\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{AC}$-$\overrightarrow{AB}$ | B. | $\overrightarrow{BD}$=$\overrightarrow{AC}$-$\frac{1}{2}$$\overrightarrow{AB}$ | C. | $\overrightarrow{BD}$=$\frac{3}{2}$$\overrightarrow{AC}$-$\overrightarrow{AB}$ | D. | $\overrightarrow{BD}$=$\overrightarrow{AC}$-$\frac{3}{2}$$\overrightarrow{AB}$ |
2.在2015年全国青运会火炬传递活动中,有编号为1,2,3,4,5的5名火炬手.若从中任选2人,则选出的火炬手的编号相连的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{10}$ | D. | $\frac{2}{5}$ |
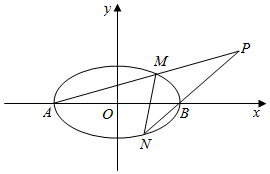 已知椭圆E:$\frac{x^2}{4}+\frac{y^2}{3}=1$的左、右顶点分别为A,B,M,N是椭圆E上异于A,B的两点,直线AM,BN交于点P(4,t).
已知椭圆E:$\frac{x^2}{4}+\frac{y^2}{3}=1$的左、右顶点分别为A,B,M,N是椭圆E上异于A,B的两点,直线AM,BN交于点P(4,t).