题目内容
7.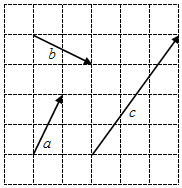 如图,网格纸上小正方形的边长为1,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),则x+y=$\frac{13}{5}$.
如图,网格纸上小正方形的边长为1,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),则x+y=$\frac{13}{5}$.
分析 作出图形,取单位向量$\overrightarrow{i},\overrightarrow{j}$,从而可用$\overrightarrow{i},\overrightarrow{j}$分别表示出向量$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$,再由$\overrightarrow{c}=x\overrightarrow{a}+y\overrightarrow{b}$,根据平面向量基本定理即可建立关于x,y的二元一次方程组,解出x,y,从而得出x+y的值.
解答 解:如图,取单位向量$\overrightarrow{i},\overrightarrow{j}$,则:
$\overrightarrow{a}=\overrightarrow{i}+2\overrightarrow{j}$,$\overrightarrow{b}=2\overrightarrow{i}-\overrightarrow{j}$,$\overrightarrow{c}=3\overrightarrow{i}+4\overrightarrow{j}$;
∴$\overrightarrow{c}=x\overrightarrow{a}+y\overrightarrow{b}=x(\overrightarrow{i}+2\overrightarrow{j})+y(2\overrightarrow{i}-\overrightarrow{j})$=$(x+2y)\overrightarrow{i}+(2x-y)\overrightarrow{j}$;
∴由平面向量基本定理得,$\left\{\begin{array}{l}{x+2y=3}\\{2x-y=4}\end{array}\right.$;
∴$\left\{\begin{array}{l}{x=\frac{11}{5}}\\{y=\frac{2}{5}}\end{array}\right.$;
∴$x+y=\frac{13}{5}$.
故答案为:$\frac{13}{5}$.
点评 考查向量加法和数乘的几何意义,向量的数乘运算,以及平面向量基本定理.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{AC}$-$\overrightarrow{AB}$ | B. | $\overrightarrow{BD}$=$\overrightarrow{AC}$-$\frac{1}{2}$$\overrightarrow{AB}$ | C. | $\overrightarrow{BD}$=$\frac{3}{2}$$\overrightarrow{AC}$-$\overrightarrow{AB}$ | D. | $\overrightarrow{BD}$=$\overrightarrow{AC}$-$\frac{3}{2}$$\overrightarrow{AB}$ |
| A. | $\frac{3}{10}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{10}$ | D. | $\frac{2}{5}$ |
| A. | $(-∞,\;-\frac{1}{2}]$ | B. | $(-∞,\;-\frac{1}{2}]∪(0,\;+∞)$ | C. | $[-\frac{1}{2},\;-\frac{1}{3}]$ | D. | $(-∞,\;-\frac{1}{3}]∪$$[-\frac{1}{2},\;0)$ |