题目内容
已知函数f(x)=|cosx|,g(x)=
,则函数F(x)=f(x)-g(x)在区间[-
,
]内的零点个数为( )
|
| 5π |
| 2 |
| 5π |
| 2 |
| A、5 | B、7 | C、9 | D、10 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:同一坐标系里作出f(x)=|cosx|,g(x)=
的图象,分析两个图象在区间[-
,
]内交点的个数,由此可得函数F(x)=f(x)-g(x)零点的个数.
|
| 5π |
| 2 |
| 5π |
| 2 |
解答:
解:函数F(x)=f(x)-g(x)的零点个数,
即函数f(x)=|cosx|与g(x)=
图象交点的个数,
同一坐标系里作出f(x)=|cosx|,g(x)=
的图象如下图所示:
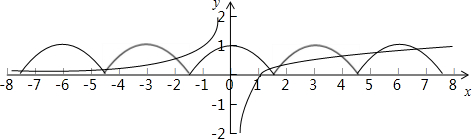
由图可得两个函数的图象在区间[-
,
]内共有9个交点,
故函数F(x)=f(x)-g(x)有9个零点,
故选:C
即函数f(x)=|cosx|与g(x)=
|
同一坐标系里作出f(x)=|cosx|,g(x)=
|
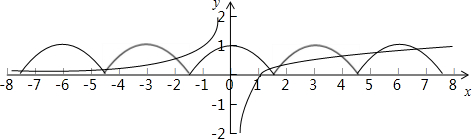
由图可得两个函数的图象在区间[-
| 5π |
| 2 |
| 5π |
| 2 |
故函数F(x)=f(x)-g(x)有9个零点,
故选:C
点评:本题求函数F(x)=f(x)-g(x)零点的个数,着重考查了余弦函数、对数函数的图象和函数的简单性质等知识,属于基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
已知α,β是两个不同的平面,?是一条直线,则下列命题中正确的是( )
| A、若α⊥β,??α,则?⊥β |
| B、若?∥α,α∥β,则?∥β |
| C、若?⊥α,?∥β,则α⊥β |
| D、若α⊥β,?⊥β,则?∥α |
定义n!=1×2×…×n.如图是求10!的程序框图,则在判断框内应填的条件是( )


| A、i<10 | B、i>10 |
| C、i≤11 | D、i≤10 |
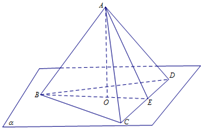 如图,正三棱锥A-BCD放置在平面α上,AD=kCD,O是底面△BCD的中心,E是CD的中点,下列说法中,错误的是( )
如图,正三棱锥A-BCD放置在平面α上,AD=kCD,O是底面△BCD的中心,E是CD的中点,下列说法中,错误的是( )A、k>
| ||||||||
B、当AD=CD=1时,将三棱锥绕直线AO旋转一周所形成的几何 体的体积是
| ||||||||
| C、动点P在截面ABE上运动,且到点B的距离与到点侧面ACD的距离相等,则点P在抛物线弧上 | ||||||||
D、当k=
|
角α的终边过点(2sin30°,-2cos30°),则cosα的值为( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知集合M={y|y=x2-1},集合N={x|y=
},则∁RM∩N=( )
| 4-x2 |
| A、(-2,-1) |
| B、[-2,-1] |
| C、[-2,1) |
| D、[-2,-1) |