题目内容
若三角形的三条边长分别为3，4，5，则将每条边长增加相同的长度后所得到的新三角形为（ ）
| A、直角三角形 | B、钝角三角形 |
| C、锐角三角形 | D、不能确定 |
考点：三角形的形状判断
专题：解三角形
分析：设三边分别为：3+x，4+x，5+x，由余弦定理可得最大角的余弦值，可判最大角为锐角，可得结论．
解答：
解：设每条边长增加相同的长度x，（x＞0）
则三边分别为：3+x，4+x，5+x，
设最长边5+x对的角为α，
由余弦定理可得cosα=
=
＞0，∴最大角为锐角，
∴新三角形为锐角三角形，
故选：C
则三边分别为：3+x，4+x，5+x，
设最长边5+x对的角为α，
由余弦定理可得cosα=
| (3+x)2+(4+x)2-(5+x)2 |
| 2(3+x)(4+x) |
=
| x |
| 2(3+x) |
∴新三角形为锐角三角形，
故选：C
点评：本题考查三角形形状的判断，涉及余弦定理的应用是，属基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
已知a，b，c，d为偶数，且0＜a＜b＜c＜d，d-a=90，a，b，c成等差数列，b，c，d成等比数列，则a+b+c+d的值为（ ）
| A、384 | B、324 |
| C、284 | D、194 |
函数y=x3-3x的极大值为M极小值为N，则M+N=（ ）
| A、）4 | B、2 | C、1 | D、0 |
如果函数f（x）=
是奇函数，那么a=（ ）
| a•3x+2a-3 |
| 3x+1 |
| A、1 | ||
B、
| ||
| C、-1 | ||
| D、-2 |
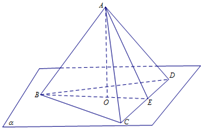如图，正三棱锥A-BCD放置在平面α上，AD=kCD，O是底面△BCD的中心，E是CD的中点，下列说法中，错误的是（ ）A、k＞
| ||||||||
B、当AD=CD=1时，将三棱锥绕直线AO旋转一周所形成的几何 体的体积是
| ||||||||
| C、动点P在截面ABE上运动，且到点B的距离与到点侧面ACD的距离相等，则点P在抛物线弧上 | ||||||||
D、当k=
|
下列函数中，x=0是极值点的函数是（ ）
| A、y=-x3 | ||
| B、y=-cosx | ||
| C、y=tanx-x | ||
D、y=
|
在极坐标系中，曲线C1：ρ（
cosθ+sinθ）=1与曲线C2：ρ=a（a＞0）的一个交点在极轴上，则a等于（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
已知全集U={1，2，3，4，5}，集合A={1，2，3}，则∁UA为（ ）
| A、{1，3，4} |
| B、{4，5} |
| C、{0，2，4} |
| D、{0，2，3，4} |