题目内容
已知三角形ABC中,AB=AC,BC=4,∠BAC=90°,
=3
,若P是BC边上的动点,则
•
的取值范围是 .
| BE |
| EC |
| AP |
| AE |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:如图所示,由AB=AC,BC=4,∠BAC=90°,可得AB=AC=2
.由
=3
,可得
=
+
.设P(x,y),则x+y=2
,0≤y≤2
.则
•
=
(y+
),即可得出.
| 2 |
| BE |
| EC |
| OE |
| 3 |
| 4 |
| OC |
| 1 |
| 4 |
| OB |
| 2 |
| 2 |
| AP |
| AE |
| 2 |
| 2 |
解答:
解:如图所示,
∵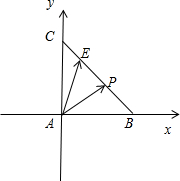 AB=AC,BC=4,∠BAC=90°,
AB=AC,BC=4,∠BAC=90°,
∴AB=AC=2
,
∵
=3
,
∴
-
=3(
-
),
∴
=
+
=(
,
).
设P(x,y),则x+y=2
,0≤y≤2
.
则
•
=
x+
y=
(x+3y)=
(2y+2
)=
(y+
)∈[2,6].
故答案为:[2,6].
∵
 AB=AC,BC=4,∠BAC=90°,
AB=AC,BC=4,∠BAC=90°,∴AB=AC=2
| 2 |
∵
| BE |
| EC |
∴
| OE |
| OB |
| OC |
| OE |
∴
| OE |
| 3 |
| 4 |
| OC |
| 1 |
| 4 |
| OB |
| ||
| 2 |
3
| ||
| 2 |
设P(x,y),则x+y=2
| 2 |
| 2 |
则
| AP |
| AE |
| ||
| 2 |
3
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| 2 |
故答案为:[2,6].
点评:本题考查了向量的坐标运算、数量积运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
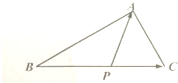 如图,已知△ABC中,A=90°,B=30°,点P在BC上运动且满足
如图,已知△ABC中,A=90°,B=30°,点P在BC上运动且满足| CP |
| CB |
| PA |
| PC |
A、
| ||
B、
| ||
C、
| ||
D、
|
一个几何体的三视图如图所示,则该几何体的体积为( )
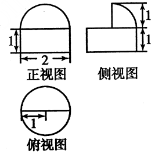

A、
| ||
B、
| ||
C、
| ||
D、
|
 某校为了解高一学生12月份的阅读情况,抽查并统计了100名同学的某一周阅读时间,绘制了频率分布直方图(如图所示),那么这100名学生中阅读时间在[8,12]小时内的人数为
某校为了解高一学生12月份的阅读情况,抽查并统计了100名同学的某一周阅读时间,绘制了频率分布直方图(如图所示),那么这100名学生中阅读时间在[8,12]小时内的人数为