题目内容
已知数列{an}中,a1=1,an+1=
(I)证明数列{a2n-
}是等比数列;
(II)若Sn是数列{an}的前n项和,求S2n.
|
(I)证明数列{a2n-
| 3 |
| 2 |
(II)若Sn是数列{an}的前n项和,求S2n.
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)设bn=a2n-
,则b1=a2-
=-
,
=
=
,由此能证明数列{a2n-
}是以-
为首项,
为公比的等比数列.
(Ⅱ)由bn=a2n-
=-
•(
)n-1=-
•(
)n,得a2n=-
•(
)n+
,从而a2n-1+a2n=-2•(
)n-6n+9,由此能求出S2n.
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 6 |
| bn+1 |
| bn |
a2n+2-
| ||
a2n-
|
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
(Ⅱ)由bn=a2n-
| 3 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
解答:
(Ⅰ)证明:设bn=a2n-
,则b1=a2-
=(
a1+1)-
=-
,
=
=
=
=
,
∴数列{a2n-
}是以-
为首项,
为公比的等比数列.
(Ⅱ)解:由(Ⅰ)得bn=a2n-
=-
•(
)n-1=-
•(
)n,
∴a2n=-
•(
)n+
,
由a2n=
a2n-1-3(2n-1),
得a2n-1=3a2n-3(2n-1)=-
•(
)n-1-6n+
,
∴a2n-1+a2n=-
•[(
)n-1+(
)n]-6n+9
=-2•(
)n-6n+9,
S2n=(a1+a2)+(a3+a4)+…+(a2n-1+a2n)
=-2[
+(
)2+…+(
)n]-6(1+2+3+…+n)+9n
=(
)n-1-3n2+6n
=(
)n-3(n-1)2+2.
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 6 |
| bn+1 |
| bn |
a2n+2-
| ||
a2n-
|
| ||||
a2n-
|
=
| ||||
a2n-
|
| 1 |
| 3 |
∴数列{a2n-
| 3 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
(Ⅱ)解:由(Ⅰ)得bn=a2n-
| 3 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∴a2n=-
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
由a2n=
| 1 |
| 3 |
得a2n-1=3a2n-3(2n-1)=-
| 1 |
| 2 |
| 1 |
| 3 |
| 15 |
| 2 |
∴a2n-1+a2n=-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
=-2•(
| 1 |
| 3 |
S2n=(a1+a2)+(a3+a4)+…+(a2n-1+a2n)
=-2[
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
=(
| 1 |
| 3 |
=(
| 1 |
| 3 |
点评:本题考查等比数列的证明,考查数列的前2n项和的求法,是中档题,解题时要认真审题,注意构造法、等比数列性质、分组求和法的合理运用.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,俯视图是半径为
某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则其侧视图的面积是( )
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
函数f(x)=xcosx2在区间[0,3]上的零点的个数为( )
| A、2 | B、3 | C、4 | D、5 |
在△ABC中,角A,B,C所对的边分别为a,b,c,c=1,B=45°,cosA=
,则b等于( )
| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
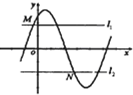 如图:M(xM,yM),N(xN,yN)分别是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与两条直线l1:y=m,l2:y=-m(A≥m≥0)的两个交点,记S=|xN-xM|,则S(m)图象大致是( )
如图:M(xM,yM),N(xN,yN)分别是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与两条直线l1:y=m,l2:y=-m(A≥m≥0)的两个交点,记S=|xN-xM|,则S(m)图象大致是( )


