题目内容
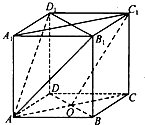 如图,在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点.
如图,在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点.(Ⅰ)求证:C1O∥平面AB1D1;
(Ⅱ)求直线BC与平面ACC1A1所成角大小.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)设A1C1∩B1D1=O1,连接AO1,由已知得四边形AOC1O1为平行四边形,由此能证明C1O∥平面AB1D1.
(Ⅱ)由已知得AA1⊥BD,AC⊥BD,从而BD⊥平面ACC1A1,∠BCO为直线BC与平面ACC1A1所成的角,由此能求出直线BC与平面ACC1A1所成角.
(Ⅱ)由已知得AA1⊥BD,AC⊥BD,从而BD⊥平面ACC1A1,∠BCO为直线BC与平面ACC1A1所成的角,由此能求出直线BC与平面ACC1A1所成角.
解答:
(Ⅰ)证明:设A1C1∩B1D1=O1,连接AO1,
∵AO
C1O1,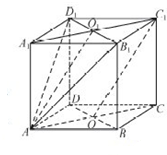
∴四边形AOC1O1为平行四边形,
∴AO1∥OC1,
又AO1?平面AB1D1,C1O不包含于平面AB1D1,
∴C1O∥平面AB1D1.
(Ⅱ)解:在正方体ABCD-A1B1C1D1中,
∵AA1⊥平面ABCD,∴AA1⊥BD,
又在正方形ABCD中,AC⊥BD,
∵AC∩AA1=A,∴BD⊥平面ACC1A1,
∴∠BCO为直线BC与平面ACC1A1所成的角,
在正方形ABCD中,由题意知∠BCO=45°,
∴直线BC与平面ACC1A1所成角为45°.
∵AO
| ∥ |
. |

∴四边形AOC1O1为平行四边形,
∴AO1∥OC1,
又AO1?平面AB1D1,C1O不包含于平面AB1D1,
∴C1O∥平面AB1D1.
(Ⅱ)解:在正方体ABCD-A1B1C1D1中,
∵AA1⊥平面ABCD,∴AA1⊥BD,
又在正方形ABCD中,AC⊥BD,
∵AC∩AA1=A,∴BD⊥平面ACC1A1,
∴∠BCO为直线BC与平面ACC1A1所成的角,
在正方形ABCD中,由题意知∠BCO=45°,
∴直线BC与平面ACC1A1所成角为45°.
点评:本题考查直线与平面平行的证明,考查直线与平面所成角的大小的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
如图,是某篮球运动员在一个赛季的30场比赛中的得分的茎叶图,则得分的中位数和众数分别为( )

| A、3和3 | B、23和3 |
| C、3和23 | D、23和23 |
下列函数中既是奇函数,又在区间(0,+∞)上单调递增的是( )
| A、y=sinx |
| B、y=-x2 |
| C、y=xlg2 |
| D、y=-x3 |
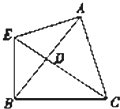 已知四边形ACBE,AB交CE于D点,BC=
已知四边形ACBE,AB交CE于D点,BC=