��Ŀ����
3��Ϊ�˶�2016��ijУ�п��ɼ����з�������60�����ϵ�ȫ��ͬѧ��������8λ�����ǵ���ѧ������������Ϊ�ٷ��ƣ���С��������60��65��70��75��80��85��90��95������������С��������72��77��80��84��88��90��93��95����1�����涨85������Ϊ���㣬����8λͬѧ��ǡ��3λͬѧ����ѧ������������Ϊ����ĸ��ʣ�
��2������8λͬѧ����ѧ����������ѧ������ʵ�϶�Ӧ���±���
| ѧ����� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ��ѧ����x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| ��������y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
| ��ѧ����z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
����y��x��z��x�����Իع鷽�̣�ϵ����ȷ��0.01������ijͬѧ����ѧ�ɼ�Ϊ50��ʱ����������������ѧ���Ƶĵ÷֣�
�ο���ʽ�����ϵ��$r=\frac{{\sum_{i=1}^n{��{{x_i}-\overline x}��}��{{y_i}-\overline y}��}}{{\sqrt{\sum_{i=1}^n{{{��{{x_i}-\overline x}��}^2}}}•\sum_{i=1}^n{{{��{{y_i}-\overline y}��}^2}}}}$��
�ع�ֱ�߷����ǣ�$\hat y=bx+a$������$b=\frac{{\sum_{i=1}^n{��{{x_i}-\overline x}����{{y_i}-\overline y}��}}}{{\sum_{i=1}^n{{{��{{x_i}-\overline x}��}^2}}}}��a=\overline y-b\overline x$��
�ο����ݣ�$\overline x=77.5��\overline y=85��\overline z=81��\sum_{i=1}^8{{{��{{x_i}-\overline x}��}^2}��1050��\sum_{i=1}^8{{{��{{y_i}-\overline y}��}^2}��456}}$��$\sum_{i=1}^8{{{��{{z_i}-\overline z}��}^2}}��550��\sum_{i=1}^8{��{{x_i}-\overline x}����{{y_i}-\overline y}����688}$��$\sum_{i=1}^8{��{{x_i}-\overline x}����{{z_i}-\overline z}����755}��\sqrt{1050}��32.4$��$\sqrt{456}��21.4��\sqrt{550}��23.5$��
���� ��1���������8λͬѧ��ǡ��3λͬѧ����ѧ������������Ϊ����Ļ����¼�����
�Լ���8λͬѧ��������������ѧ�����ֱ��Ӧ�����¼�������������ĸ���ֵ��
��2���ٱ���y��x��z��x�����ϵ�����ó���������ѧ����ѧ����ѧ�ɼ����Ǹ߶�����أ�
�����y��x��z��x�����Իع鷽�̣��ɴ˼���x=50ʱy��z��ֵ���ɣ�
��� �⣺��1����8λͬѧ��ǡ��3λͬѧ����ѧ������������Ϊ���㣬
����Ҫ�ȴ�����4 �����������ѡ��3������ѧ������Ӧ��
��ͬ��������${C}_{4}^{3}$${A}_{3}^{3}$����${A}_{4}^{3}$����
Ȼ��ʣ�µ�5����ѧ�������������������Ӧ����ͬ��������$A_5^5$��
���ݳ˷�ԭ�������������IJ�ͬ������$C_4^3A_3^3A_5^5$��
��8λͬѧ��������������ѧ�����ֱ��Ӧ��������$A_8^8$��
������ĸ���Ϊ$P=\frac{C_4^3A_3^3A_5^5}{A_8^8}=\frac{1}{14}$��
��2���ٱ���y��x��z��x�����ϵ���ֱ���
$r=\frac{688}{32.4��21.4}��0.99��r'=\frac{755}{32.4��23.5}��0.99$��
���Կ�������������ѧ����ѧ����ѧ�ɼ����Ǹ߶�����أ�
����y��x��z��x�����Իع鷽�̷ֱ���$\hat y=bx+a��\hat z=b'x+a'$��
�������������ݣ������
$b=\frac{688}{1050}=0.66��a=85-0.66��77.5=33.85$��
$b'=\frac{755}{1050}=0.72��a'=81-0.72��77.5=25.20$��
����y��x��z��x�Ļع鷽�̷ֱ���
$\hat y=0.66x+33.85$��$\hat z=0.72x+25.20��$��
��x=50ʱ��$\hat y=66.85��\hat z=61.2$��
�൱��������ѧΪ50��ʱ������������ѧ�ɼ��ֱ�ԼΪ66.85�֡�61.2�֣�
���� ���⿼���˹ŵ���͵ĸ��������Իع鷽�̵�Ӧ�����⣬�ǻ�����Ŀ��

| A�� | ��-2��1�� | B�� | ��1��4�� | C�� | {2��3} | D�� | {-1��0} |

| A�� | 74 | B�� | 75 | C�� | 76 | D�� | 77 |
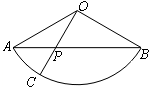 ��ͼ������AOB��Բ�Ľ�Ϊ120�㣬��P����AB�ϣ���$AP=\frac{1}{3}AB$���ӳ�OP����AB��C����������AOB��Ͷ�㣬��õ���������AOC�ڵĸ���Ϊ��������
��ͼ������AOB��Բ�Ľ�Ϊ120�㣬��P����AB�ϣ���$AP=\frac{1}{3}AB$���ӳ�OP����AB��C����������AOB��Ͷ�㣬��õ���������AOC�ڵĸ���Ϊ��������| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{2}{7}$ | D�� | $\frac{3}{8}$ |
 ij�����������ͼ��ͼ��ʾ����ü���������Ϊ��������
ij�����������ͼ��ͼ��ʾ����ü���������Ϊ��������| A�� | $\frac{��}{3}$ | B�� | $\frac{7��}{6}$ | C�� | �� | D�� | $\frac{5��}{6}$ |