题目内容
14.已知函数$f(x)=\frac{1}{2}{x^2}+(1-a)x-alnx\;,\;a∈R$.(1)若f(x)存在极值点为1,求a的值;
(2)若f(x)存在两个不同零点x1,x2,求证:x1+x2>2.
分析 (1)求出$f'(x)=x+1-a-\frac{a}{x}$,利用f(x)存在极值点为1,结合f'(1)=0,求出a.
(2)求出$f'(x)=x+1-a-\frac{a}{x}=(x+1)(1-\frac{a}{x})(x>0)$,通过①当a≤0时,②当a>0时,判断函数的单调性求出函数的极值,所以当x=a时,f(x)取得极小值f(a),利用f(x)存在两个不同零点x1,x2,f(a)<0,作y=f(x)关于直线x=a的对称曲线g(x)=f(2a-x),令h(x)=g(x)-f(x)=f(2a-x)-f(x),求出导数,利用函数的单调性,最值推出结果.
解答 (本小题满分12分)
解:(1)$f'(x)=x+1-a-\frac{a}{x}$,因为f(x)存在极值点为1,所以f'(1)=0,即2-2a=0,a=1,经检验符合题意,所以a=1.(4分)
(2)$f'(x)=x+1-a-\frac{a}{x}=(x+1)(1-\frac{a}{x})(x>0)$
①当a≤0时,f'(x)>0恒成立,所以f(x)在(0,+∞)上为增函数,不符合题意;
②当a>0时,由f'(x)=0得x=a,
当x>a时,f'(x)>0,所以f(x)为增函数,当0<x<a时,f'(x)<0,所f(x)为减函数,
所以当x=a时,f(x)取得极小值f(a)
又因为f(x)存在两个不同零点x1,x2,所以f(a)<0,即$\frac{1}{2}{a^2}+(1-a)a-alna<0$
整理得$lna>1-\frac{1}{2}a$,
作y=f(x)关于直线x=a的对称曲线g(x)=f(2a-x),
令$h(x)=g(x)-f(x)=f(2a-x)-f(x)=2a-2x-aln\frac{2a-x}{x}$$h'(x)=-2+\frac{{2{a^2}}}{(2a-x)x}=-2+\frac{{2{a^2}}}{{-{{(x-a)}^2}+{a^2}}}≥0$所以h(x)在(0,2a)上单调递增,
不妨设x1<a<x2,则h(x2)>h(a)=0,即g(x2)=f(2a-x2)>f(x2)=f(x1),
又因为2a-x2∈(0,a),x1∈(0,a),且f(x)在(0,a)上为减函数,
故2a-x2<x1,即x1+x2>2a,又$lna>1-\frac{1}{2}a$,易知a>1成立,故x1+x2>2.(12分)
点评 本小题主要考查函数与导数的知识,具体涉及到导数的运算,用导数来研究函数的单调性等,考查学生解决问题的综合能力.


| A. | 74 | B. | 75 | C. | 76 | D. | 77 |
| A. | {0,1,2} | B. | {1,2} | C. | {1,2,4} | D. | {1,4} |
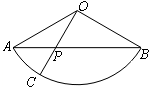 如图,扇形AOB的圆心角为120°,点P在弦AB上,且$AP=\frac{1}{3}AB$,延长OP交弧AB于C.现向扇形AOB内投点,则该点落在扇形AOC内的概率为( )
如图,扇形AOB的圆心角为120°,点P在弦AB上,且$AP=\frac{1}{3}AB$,延长OP交弧AB于C.现向扇形AOB内投点,则该点落在扇形AOC内的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{7}$ | D. | $\frac{3}{8}$ |
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如右图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如右图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.(1)完成2×2列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
(2)为了改良玉米品种,现采用分层抽样的方式从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交实验,选取的植株均为矮茎的概率是多少?
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
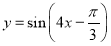 的图像,只需要将函数
的图像,只需要将函数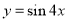 的图像( )
的图像( ) 个单位 B.向右平移
个单位 B.向右平移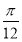 个单位
个单位 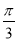 个单位 D.向右平移
个单位 D.向右平移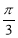 个单位
个单位