题目内容
4.圆(x-2)2+y2=4关于直线$y=\frac{{\sqrt{3}}}{3}x$对称的圆的方程是( )| A. | ${(x-\sqrt{3})^2}+{(y-1)^2}=4$ | B. | ${(x-\sqrt{2})^2}+{(y-\sqrt{2})^2}=4$ | C. | x2+(y-2)2=4 | D. | ${(x-1)^2}+{(y-\sqrt{3})^2}=4$ |
分析 求出圆(x-2)2+y2=4的圆心关于直线$y=\frac{{\sqrt{3}}}{3}x$对称的坐标,即可得出结论.
解答 解:设圆(x-2)2+y2=4的圆心关于直线$y=\frac{{\sqrt{3}}}{3}x$对称的坐标为(a,b),则$\left\{\begin{array}{l}{\frac{b}{a-2}•\frac{\sqrt{3}}{3}=-1}\\{\frac{b}{2}=\frac{\sqrt{3}}{3}•\frac{a+2}{2}}\end{array}\right.$,
∴a=1,b=$\sqrt{3}$,
∴圆(x-2)2+y2=4的圆心关于直线$y=\frac{{\sqrt{3}}}{3}x$对称的坐标为$(1,\sqrt{3})$,
从而所求圆的方程为${(x-1)^2}+{(y-\sqrt{3})^2}=4$.
故选D.
点评 本题考查直线与圆的相关知识.求出圆(x-2)2+y2=4的圆心关于直线$y=\frac{{\sqrt{3}}}{3}x$对称的坐标是关键.

练习册系列答案
相关题目
17.已知i是虚数单位,若复数$\frac{z}{1+i}=2i$满足,则复数z对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.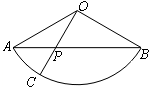 如图,扇形AOB的圆心角为120°,点P在弦AB上,且$AP=\frac{1}{3}AB$,延长OP交弧AB于C.现向扇形AOB内投点,则该点落在扇形AOC内的概率为( )
如图,扇形AOB的圆心角为120°,点P在弦AB上,且$AP=\frac{1}{3}AB$,延长OP交弧AB于C.现向扇形AOB内投点,则该点落在扇形AOC内的概率为( )
 如图,扇形AOB的圆心角为120°,点P在弦AB上,且$AP=\frac{1}{3}AB$,延长OP交弧AB于C.现向扇形AOB内投点,则该点落在扇形AOC内的概率为( )
如图,扇形AOB的圆心角为120°,点P在弦AB上,且$AP=\frac{1}{3}AB$,延长OP交弧AB于C.现向扇形AOB内投点,则该点落在扇形AOC内的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{7}$ | D. | $\frac{3}{8}$ |
12.从数字1,2,3,4,5中,随机抽取3个数字(允许重复)组成一个三位数,其各位数字之和等于12的概率为( )
| A. | $\frac{2}{25}$ | B. | $\frac{13}{125}$ | C. | $\frac{18}{125}$ | D. | $\frac{9}{125}$ |
 对于任意
对于任意 恒成立;
恒成立;  ,如果命题“
,如果命题“ 为真,
为真, 为假”,求实数
为假”,求实数 的取值范围.
的取值范围.