题目内容
8．下列命题中正确的是（ ）| A． | 若直线a在平面α外，则直线a与平面内任何一点都只可以确定一个平面 | |
| B． | 若a，b分别与两条异面直线都相交，则a，b是异面直线 | |
| C． | 若直线a平行于直线b，则a平行于过b的任何一个平面 | |
| D． | 若a，b是异面直线，则经过a且与b垂直的平面可能不存在 |
分析 根据空间直线和平面的位置关系分别进行判断即可得到结论．
解答 解：A．当直线a与α相交时，设a∩α=A，当直线a与平面内内的点A时，此时有无数个平面，故A错误，
B．若a，b分别与两条异面直线都相交，则a，b是异面直线或者a，b相交，故B错误，
C．若直线a平行于直线b，则a平行于过b的任何一个平面或a在过b的平面内，故C错误，
D．如果直线a与直线b垂直时，根据线面垂直的判定定理可知存在唯一一个平面满足条件；
当直线a与直线b不垂直时，如果找到过a且与b垂直的平面，则b垂直平面内任一直线，而a在平面内，则直线a与直线b垂直，这与条件矛盾，故不存在，
故若a，b是异面直线，则经过a且与b垂直的平面可能不存在，正确，
故选：D．
点评 本题主要考查命题的真假判断，根据空间直线和平面的位置关系是解决本题的关键．
练习册系列答案
相关题目
18．已知$\overrightarrow a=（-1，\;3）$，$\overrightarrow b=（1，\;-1）$，那么$\overrightarrow a，\overrightarrow b$夹角的余弦值（ ）
| A． | $-\frac{{2\sqrt{5}}}{5}$ | B． | $-\frac{{\sqrt{5}}}{5}$ | C． | -2 | D． | -$\frac{1}{3}$ |
石嘴山市在每年的春节后，市政府都会发动公务员参与到植树活动中去．林管部门在植树前，为保证树苗的质量，都会在植树前对树苗进行检测．现从甲乙两种树苗中各抽测了10株树苗的高度，量出的高度如下（单位：厘米）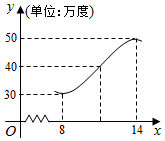
如图，某地夏天从8～14时用电量变化曲线近似满足函数y=Asin（ωx+φ）+b（ω＞0，0＜φ＜π）．