题目内容
13.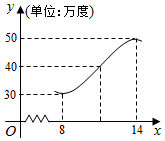 如图,某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+b(ω>0,0<φ<π).
如图,某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+b(ω>0,0<φ<π).(1)指出这一时间段的最大用电量及最小用电量;
(2)求出A,ω,φ,b的值,写出这段曲线的函数解析式.
分析 (1)由图可知这一天的最大用电量及最小用电量;
(2)由图可求得A,ω,b,再由f(8)=30可求得φ.
解答 解:(1)最大用电量为50万度,最小用电量为30万度.
(2)观察图象可知,从8~14时的图象是y=Asin(ωx+φ)+b的半个周期的图象.
∴$A=\frac{1}{2}×(50-30)=10$.$b=\frac{1}{2}×(50+30)=40$.
∵$\frac{T}{2}=14-8=\frac{1}{2}•\frac{2π}{ω}$,
∴$ω=\frac{π}{6}$.
∴$y=10sin(\frac{π}{6}x+φ)+40$,
将x=8,y=30代入上式,解得$φ=\frac{π}{6}$,
∴所求解析式为$y=10sin(\frac{π}{6}x+\frac{π}{6})+40,x∈[8,14]$.
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求φ是难点,考查观察、分析与运算能力,属于中档题.

练习册系列答案
相关题目
1.下列说法正确的是( )
| A. | $?x∈{R}\;,\;\root{3}{x}+1>0$ | |
| B. | 在线性回归分析中,如果两个变量的相关性越强,则相关系数r就越接近于1 | |
| C. | p∨q为真命题,则命题p和q均为真命题 | |
| D. | 命题“$?{x_0}∈{R}\;,\;x_0^2-{x_0}>0$”的否定是“?x∈R,x2-x≤0” |
8.下列命题中正确的是( )
| A. | 若直线a在平面α外,则直线a与平面内任何一点都只可以确定一个平面 | |
| B. | 若a,b分别与两条异面直线都相交,则a,b是异面直线 | |
| C. | 若直线a平行于直线b,则a平行于过b的任何一个平面 | |
| D. | 若a,b是异面直线,则经过a且与b垂直的平面可能不存在 |
18.某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | $\frac{1}{3}+2π$ | B. | $\frac{{11+\sqrt{2}}}{2}π+1$ | C. | $\frac{{11π+\sqrt{2}}}{2}$ | D. | $\frac{11π}{2}+\sqrt{2}π$ |
5.若cosθ<0,且$cosθ-sinθ=\sqrt{1-sin2θ}$,那么θ是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |