Question

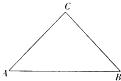某公司为其中公司成立十五周年，回馈政府的支持和帮助，决定于市中心新建一三角形绿地广场，如图，△ABC为一个等腰三角形性状的绿地，腰CA的长为3（百米），底AB的长为4（百米），现决定在绿地内筑一条笔直的小路EF（宽度不计），将该绿地分成一个四边形和一个三角形，设分成的四边形和三角形的周长相等、面积分别为S₁和S₂．
（1）若小路一端E为AC的中点，求此时小路的长度；
（2）求

S1

S2

的最小值．

Answer 1

考点：函数的最值及其几何意义

专题：计算题,应用题

分析：（1）根据题意可知F不在BC上，根据余弦定理求出cosA的值，然后根据余弦定理求出EF的长即可；
（2）若E、F分别在AC和AB上，设AE=x，AF=y，然后利用三角形的面积公式求出S₂和S₁=S_三角形ABC-S₂=，再根据基本不等式求出比值的最值即可，若E、F分别在AC和BC上，设CE=x，CF=y，同上根据基本不等式求出比值的最值即可．

解答： 解：（1）因为：AE=CE=

3

2

，AE+4＞CE+3 所以F不在BC上，
AE+AF+EF=CE+CB+FB+EF，
所以AE=CE，AF=CB+BF，4-BF=BF+3，BF=

1

2

cosA=

AC2+AB2-BC2

2AC×AB

=

2

3

，所以EF²=AE²+AF²-2AE×AF×cosA=

15

2

，
所以EF=

30

2

．
∴E为AC中点时，此时小路的长度为

30

2

．
（2）若E、F分别在AC和AB上，sinA=

5

3

，
设AE=x，AF=y，
所以S₂=

1

2

xysinA=

5 xy

6

，
S₁=S_三角形ABC-S₂=2

5

-S₂，
因为x+y=3-x+4-y+3，
所以x+y=5，

S1

S2

=

2 5 -S2

5 xy 6

≥

48

25

-1，xy≤(

x+y

2

)2=

25

4

，
当且仅当x=y=

5

2

时取等号，
所以

S1

S2

=

23

25

，当且仅当x=y=

5

2

时取等号，最小值是

23

25

．
若E、F分别在AC和BC上，

c

sinC

=

a

sinA

，sinC=

4 5

9

设CE=x，CF=y
同上可得

S1

S2

≥

11

25

当且仅当x=y=

5

2

取等号
若E、F分别在AC和BC上，最小值是

11

25

．

点评：本题主要考查了解三角形的实际应用，以及利用基本不等式求最值问题，同时考查了分类讨论的思想，属于中档题．