题目内容
已知椭圆中心在原点,左焦点与双曲线x2-y2=2的左顶点重合,离心率e=
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)已知直线l与椭圆相交于P,Q两点,O为坐标原点,若OP⊥OQ,试探究点O到直线l的距离是否为定值?若是,求出这个定值;若不是,说明理由.
| ||
| 3 |
(Ⅰ)求椭圆的标准方程;
(Ⅱ)已知直线l与椭圆相交于P,Q两点,O为坐标原点,若OP⊥OQ,试探究点O到直线l的距离是否为定值?若是,求出这个定值;若不是,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)设出椭圆的标准方程,由双曲线方程求出c,结合离心率求得a,再由隐含条件求出b,则椭圆方程可求;
(Ⅱ)当直线l的斜率存在时,设直线l的方程为y=kx+m,点P(x1,y1),Q(x2,y2),联立直线方程和椭圆方程得到关于x的一元二次方程,利用根与系数关系求得P,Q两点横纵坐标的积,由OP⊥OQ列式求得k与m的关系,然后由点到直线的距离公式求出点O到直线l的距离;当直线l的斜率不存在时,由椭圆的对称性结合OP⊥OQ直接求得P,Q的坐标,求得点O到直线l的距离.
(Ⅱ)当直线l的斜率存在时,设直线l的方程为y=kx+m,点P(x1,y1),Q(x2,y2),联立直线方程和椭圆方程得到关于x的一元二次方程,利用根与系数关系求得P,Q两点横纵坐标的积,由OP⊥OQ列式求得k与m的关系,然后由点到直线的距离公式求出点O到直线l的距离;当直线l的斜率不存在时,由椭圆的对称性结合OP⊥OQ直接求得P,Q的坐标,求得点O到直线l的距离.
解答:
解:(Ⅰ)设椭圆方程为
+
=1(a>b>0),
∵双曲线x2-y2=2的左顶点为(-
,0),∴c=
,
由e=
=
得a=
c=
,b2=a2-c2=1,
故椭圆的方程为
+y2=1;
(Ⅱ)当直线l的斜率存在时,设直线l的方程为
y=kx+m,点P(x1,y1),Q(x2,y2),
由
整理得(1+3k2)x2+6kmx+3m2-3=0.
∴x1+x2=
,x1x2=
,
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=k2•
+km•
+m2=
.
∵
⊥
,
∴x1x2+y1y2=
=0,
即4m2-3k2-3=0,∴m2=
.
设原点O到直线l的距离为d,
则d=
=
=
=
.
当直线l的斜率不存在时,
∵
⊥
,根据椭圆的对称性,不妨设直线OP,OQ的方程分别为y=x,y=-x,
可得P(-
,-
),Q(-
,
)或P(
,
),Q(
,-
).
此时,原点O到直线l的距离仍为
.
综上可得,点O到直线l的距离为定值
.
| x2 |
| a2 |
| y2 |
| b2 |
∵双曲线x2-y2=2的左顶点为(-
| 2 |
| 2 |
由e=
| c |
| a |
| ||
| 3 |
| 3 | ||
|
| 3 |
故椭圆的方程为
| x2 |
| 3 |
(Ⅱ)当直线l的斜率存在时,设直线l的方程为
y=kx+m,点P(x1,y1),Q(x2,y2),
由
|
∴x1+x2=
| 3m2-3 |
| 1+3k2 |
| -6km |
| 1+3k2 |
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=k2•
| 3m2-3 |
| 1+3k2 |
| -6km |
| 1+3k2 |
| m2-3k2 |
| 1+3k2 |
∵
| OP |
| OQ |
∴x1x2+y1y2=
| 4m2-3k2-3 |
| 1+3k2 |
即4m2-3k2-3=0,∴m2=
| 3k2+3 |
| 4 |
设原点O到直线l的距离为d,
则d=
| |m| | ||
|
|
|
| ||
| 2 |
当直线l的斜率不存在时,
∵
| OP |
| OQ |
可得P(-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
此时,原点O到直线l的距离仍为
| ||
| 2 |
综上可得,点O到直线l的距离为定值
| ||
| 2 |
点评:本题主要考查了直线与椭圆的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系解题,是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考试具备较强的运算推理的能力,是压轴题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
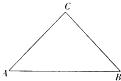 某公司为其中公司成立十五周年,回馈政府的支持和帮助,决定于市中心新建一三角形绿地广场,如图,△ABC为一个等腰三角形性状的绿地,腰CA的长为3(百米),底AB的长为4(百米),现决定在绿地内筑一条笔直的小路EF(宽度不计),将该绿地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2.
某公司为其中公司成立十五周年,回馈政府的支持和帮助,决定于市中心新建一三角形绿地广场,如图,△ABC为一个等腰三角形性状的绿地,腰CA的长为3(百米),底AB的长为4(百米),现决定在绿地内筑一条笔直的小路EF(宽度不计),将该绿地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2. 如图,在平面直角坐标系xoy中,椭圆
如图,在平面直角坐标系xoy中,椭圆