题目内容
求下列函数值域y=
(1≤x≤2).
| 2x2+2x+5 |
| x2+x+1 |
考点:函数的值域
专题:函数的性质及应用
分析:变形函数y=
=2+
,由1≤x≤2,可得3≤(x+
)2+
≤7,即可得出函数的值域.
| 2x2+2x+5 |
| x2+x+1 |
| 3 | ||||
(x+
|
| 1 |
| 2 |
| 3 |
| 4 |
解答:
解:∵函数y=
=2+
,
∵1≤x≤2,∴3≤(x+
)2+
≤7,
∴
≤
≤1,
∴
≤y≤3.
∴函数的值域y∈[
,3].
| 2x2+2x+5 |
| x2+x+1 |
| 3 | ||||
(x+
|
∵1≤x≤2,∴3≤(x+
| 1 |
| 2 |
| 3 |
| 4 |
∴
| 3 |
| 7 |
| 3 | ||||
(x+
|
∴
| 17 |
| 7 |
∴函数的值域y∈[
| 17 |
| 7 |
点评:本题考查了二次函数与反比例函数的单调性、函数的值域,属于基础题.

练习册系列答案
相关题目
已知全集U={2011,2012,2013,2014,2015},M={2011,2012,2013},则∁UM=( )
| A、{2014} |
| B、{2014,2015} |
| C、{2011,2012,2013} |
| D、{2011,2012,2013,2014,2015} |
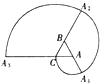 如图,一条螺旋线是用以下方法画成的:△ABC是边长为1的正三角形,曲线CA1,A1A2,A2A3是分别以A、B、C为圆心,AC、BA1、CA2为半径画的圆弧,曲线CA1A2A3称为螺旋线的第一圈,然后又以A为圆心,AA3为半径画圆弧…这样画到第n圈,则所得螺旋线的长度ln为( )
如图,一条螺旋线是用以下方法画成的:△ABC是边长为1的正三角形,曲线CA1,A1A2,A2A3是分别以A、B、C为圆心,AC、BA1、CA2为半径画的圆弧,曲线CA1A2A3称为螺旋线的第一圈,然后又以A为圆心,AA3为半径画圆弧…这样画到第n圈,则所得螺旋线的长度ln为( )| A、(3n2+n)π | ||
| B、(3n2-n+1)π | ||
C、
| ||
D、
|
若a>b>0,且a+b=1,则下列式子中最大的是( )
| A、log2a+log2b+1 |
| B、log2a |
| C、log2(a2+b2) |
| D、-1 |
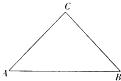 某公司为其中公司成立十五周年,回馈政府的支持和帮助,决定于市中心新建一三角形绿地广场,如图,△ABC为一个等腰三角形性状的绿地,腰CA的长为3(百米),底AB的长为4(百米),现决定在绿地内筑一条笔直的小路EF(宽度不计),将该绿地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2.
某公司为其中公司成立十五周年,回馈政府的支持和帮助,决定于市中心新建一三角形绿地广场,如图,△ABC为一个等腰三角形性状的绿地,腰CA的长为3(百米),底AB的长为4(百米),现决定在绿地内筑一条笔直的小路EF(宽度不计),将该绿地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2.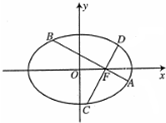 如图,在平面直角坐标系xoy中,椭圆
如图,在平面直角坐标系xoy中,椭圆