题目内容
8.已知向量$\overrightarrow{a}$=(sinθ,1),$\overrightarrow{b}$=(-sinθ,0),$\overrightarrow{c}$=(cosθ,-1),且(2$\overrightarrow{a}$-$\overrightarrow{b}$)∥$\overrightarrow{c}$,则tanθ等于-$\frac{2}{3}$.分析 2$\overrightarrow{a}$-$\overrightarrow{b}$=(3sinθ,2),利用向量共线定理即可得出.
解答 解:2$\overrightarrow{a}$-$\overrightarrow{b}$=(3sinθ,2),
∵(2$\overrightarrow{a}$-$\overrightarrow{b}$)∥$\overrightarrow{c}$,∴-3sinθ-2cosθ=0,
解得tanθ=-$\frac{2}{3}$.
故答案为:-$\frac{2}{3}$.
点评 本题考查了向量共线定理、三角函数求值,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
18.已知复数z1=1-i,z2=-2+3i,则复数$\frac{{i•{z_2}}}{z_1}$对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.已知一几何体的三视图如图所示,则该几何体的表面积为( )
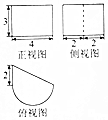

| A. | 14+6$\sqrt{5}$+10π | B. | 14+6$\sqrt{5}$+20π | C. | 12+12π | D. | 26+6$\sqrt{5}$+10π |
20.高考结束后高三的8名同学准备拼车去旅游,其中一班、二班、三班、四班每班各两名,分乘甲、乙两辆汽车,每车限坐4名同学(乘同一辆车的4名同学不考虑位置,)其中一班两位同学是孪生姐妹,需乘同一辆车,则乘坐甲车的4名同学中恰有2名同学是来自同一班的乘坐方式共有( )
| A. | 18种 | B. | 24种 | C. | 48种 | D. | 36种 |
9.已知命题p:?x0∈R,使2${\;}^{{x}_{0}}$+2${\;}^{-{x}_{0}}$=1;命题q:?x∈R,都有lg(x2+2x+3)>0.下列结论中正确的是( )
| A. | 命题“¬p∧q”是真命题 | B. | 命题“p∧¬q”是真命题 | ||
| C. | 命题“p∧q”是真命题 | D. | 命题“¬p∨¬q”是假命题 |
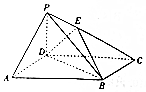 如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DBA=30°,$\sqrt{3}$AB=2BD,PD=AD,PD⊥底面ABCD,E为PC上一点,且PE=$\frac{1}{2}$EC.
如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DBA=30°,$\sqrt{3}$AB=2BD,PD=AD,PD⊥底面ABCD,E为PC上一点,且PE=$\frac{1}{2}$EC.