题目内容
17.已知P(0,1)是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上一点,点P到椭圆C的两个焦点的距离之和为2$\sqrt{2}$.(Ⅰ)求椭圆C的方程;
(Ⅱ)设A,B是椭圆C上异于点P的两点,直线PA与直线x=4交于点M,是否存在点A,使得S△ABP=$\frac{1}{2}{S_{△ABM}}$?若存在,求出点A的坐标;若不存在,请说明理由.
分析 (Ⅰ)由椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点P(0,1)可得b=1,然后求解a,即可求解椭圆的方程.
(Ⅱ)设A(m,n),直线PA的方程为:$y=\frac{n-1}{m}x+1$,求出M$({4,\frac{4n-4}{m}+1})$,通过${S_{△ABP}}=\frac{1}{2}{S_{△ABM}}$等价于$\frac{{|{PA}|}}{{|{PM}|}}=\frac{1}{3}$且点A在y轴的右侧,党的$\frac{{|{{x_A}-{x_P}}|}}{{|{{x_M}-{x_P}}|}}=\frac{|m|}{4}=\frac{1}{3}$,求出A($\frac{4}{3}$,$±\frac{1}{3}$),可得结果.
解答 (本小题共14分)
解:(Ⅰ)由椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点P(0,1)可得b=1,
又点P到两焦点距离和为$2\sqrt{2}$,可得$a=\sqrt{2}$,
所以椭圆C的方程$\frac{x^2}{2}+{y^2}=1$.…(4分)
(Ⅱ)设A(m,n),依题意得:直线PA的斜率存在,
则直线PA的方程为:$y=\frac{n-1}{m}x+1$,
令x=4,$y=\frac{4n-4}{m}+1$,即M$({4,\frac{4n-4}{m}+1})$,
又${S_{△ABP}}=\frac{1}{2}{S_{△ABM}}$等价于$\frac{{|{PA}|}}{{|{PM}|}}=\frac{1}{3}$且点A在y轴的右侧,
从而$\frac{{|{{x_A}-{x_P}}|}}{{|{{x_M}-{x_P}}|}}=\frac{|m|}{4}=\frac{1}{3}$,
因为点A在y轴的右侧,
所以$\frac{m}{4}=\frac{1}{3}$,解得 $m=\frac{4}{3}$,
由点A在椭圆上,解得:$n=±\frac{1}{3}$,
于是存在点A($\frac{4}{3}$,$±\frac{1}{3}$),使得${S_{△ABP}}=\frac{1}{2}{S_{△ABM}}$.…(14分)
点评 本题考查椭圆的简单性质以及椭圆方程的求法,存在性问题的解决方法,考查转化思想以及计算能力.

 如图,在棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为的A1B1中点O,AC=BC=AA1,∠ACB=90°.
如图,在棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为的A1B1中点O,AC=BC=AA1,∠ACB=90°.(1)求证:AB⊥平面OCC1;
(2)求二面角A-CC1-B的正弦值.
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
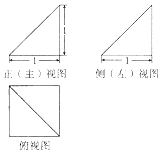
| A. | 4π | B. | 3π | C. | 12π | D. | 8π |