题目内容
20.高考结束后高三的8名同学准备拼车去旅游,其中一班、二班、三班、四班每班各两名,分乘甲、乙两辆汽车,每车限坐4名同学(乘同一辆车的4名同学不考虑位置,)其中一班两位同学是孪生姐妹,需乘同一辆车,则乘坐甲车的4名同学中恰有2名同学是来自同一班的乘坐方式共有( )| A. | 18种 | B. | 24种 | C. | 48种 | D. | 36种 |
分析 分类讨论,第一类,一班的2名同学在甲车上;第二类,一班的2名同学不在甲车上,再利用组合知识,问题得以解决.
解答 解:由题意,第一类,一班的2名同学在甲车上,甲车上剩下两个要来自不同的班级,从三个班级中选两个为C32=3,然后分别从选择的班级中再选择一个学生为C21C21=4,故有3×4=12种.
第二类,一班的2名同学不在甲车上,则从剩下的3个班级中选择一个班级的两名同学在甲车上,为C31=3,然后再从剩下的两个班级中分别选择一人为C21C21=4,这时共有3×4=12种,
根据分类计数原理得,共有12+12=24种不同的乘车方式,
故选:B.
点评 本题考查计数原理的应用,考查组合知识,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
1.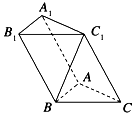 如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,若P为三角形A1B1C1
如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,若P为三角形A1B1C1
内一点(不含边界),则点P在底面ABC的投影可能在( )
 如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,若P为三角形A1B1C1
如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,若P为三角形A1B1C1内一点(不含边界),则点P在底面ABC的投影可能在( )
| A. | △ABC的内部 | B. | △ABC的外部 | C. | 直线AB上 | D. | 以上均有可能 |
 已知函数f(x)=|x+1|-|x-3|.
已知函数f(x)=|x+1|-|x-3|.