题目内容
18.已知复数z1=1-i,z2=-2+3i,则复数$\frac{{i•{z_2}}}{z_1}$对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数的运算法则、几何意义即可得出.
解答 解:复数$\frac{{i•{z_2}}}{z_1}$=$\frac{i(-2+3i)}{1-i}$=$\frac{(-3-2i)(1+i)}{(1-i)(1+i)}$=$\frac{-1-5i}{2}$对应的点$(-\frac{1}{2},-\frac{5}{2})$在第三象限.
故选:C.
点评 本题考查了复数的运算法则、几何意义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知集合A={x|$\frac{1-x}{1+x}$>0},B={x|lg(x+9)<1},则A∩B=( )
| A. | (-1,1) | B. | (-∞,1) | C. | {0} | D. | {-1,0,1} |
3.运行如图所示的程序框图,若输出的y值为$-\sqrt{2}$,则判断框中应填写的条件是( )
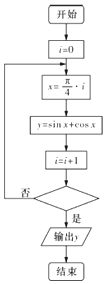

| A. | i>5? | B. | i>3? | C. | i>6? | D. | i>4? |
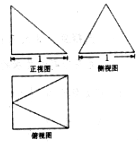
 如图,在棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为的A1B1中点O,AC=BC=AA1,∠ACB=90°.
如图,在棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为的A1B1中点O,AC=BC=AA1,∠ACB=90°.