题目内容
19.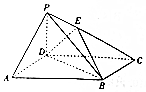 如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DBA=30°,$\sqrt{3}$AB=2BD,PD=AD,PD⊥底面ABCD,E为PC上一点,且PE=$\frac{1}{2}$EC.
如图所示,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠DBA=30°,$\sqrt{3}$AB=2BD,PD=AD,PD⊥底面ABCD,E为PC上一点,且PE=$\frac{1}{2}$EC.(1)证明:PA⊥BD;
(2)若AD=$\sqrt{6}$,求三棱锥E-CBD的体积.
分析 (1)在△ABD中,不妨设AB=2,BD=$\sqrt{3}$,由余弦定理可得AD,则AD2+BD2=BA2,从而得到BD⊥AD,结合PD⊥底面ABCD,得BD⊥PD,再由线面垂直的判定可得BD⊥平面PAD,则PA⊥BD;
(2)过E作EF⊥CD于F,则三棱锥E-CBD的高为EF,由已知可得EF.再由(1)知BD,代入三棱锥E-CBD的体积公式求解.
解答 (1)证明:在△ABD中,由余弦定理可得:AD2=BA2+BD2-2BA•BD•cos∠DBA,
不妨设AB=2,则由已知$\sqrt{3}$AB=2BD,得BD=$\sqrt{3}$,
∴$A{D}^{2}={2}^{2}+(\sqrt{3})^{2}-2×2×\sqrt{3}×\frac{\sqrt{3}}{2}=1$,则AD2+BD2=BA2,
∴∠ADB=90°,即BD⊥AD,
又PD⊥底面ABCD,∴BD⊥PD,而AD∩PD=D,
∴BD⊥平面PAD,则PA⊥BD;
(2)解:过E作EF⊥CD于F,则三棱锥E-CBD的高为EF,
由已知可得EF=$\frac{2}{3}PD=\frac{2}{3}AD=\frac{2\sqrt{6}}{3}$.
由(1)知BD=AD$•tan60°=3\sqrt{2}$,
∴三棱锥E-CBD的体积V=$\frac{1}{3}{S}_{△CBD}•EF=\frac{1}{3}×\frac{1}{2}×\sqrt{6}×3\sqrt{2}×\frac{2\sqrt{6}}{3}$=$2\sqrt{2}$.
点评 本题考查直线与平面垂直的判定和性质,考查空间想象能力和思维能力,考查棱锥体积的求法,是中档题.

练习册系列答案
相关题目
7. 如图,在棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为的A1B1中点O,AC=BC=AA1,∠ACB=90°.
如图,在棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为的A1B1中点O,AC=BC=AA1,∠ACB=90°.
(1)求证:AB⊥平面OCC1;
(2)求二面角A-CC1-B的正弦值.
 如图,在棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为的A1B1中点O,AC=BC=AA1,∠ACB=90°.
如图,在棱柱ABC-A1B1C1中,点C在平面A1B1C1内的射影点为的A1B1中点O,AC=BC=AA1,∠ACB=90°.(1)求证:AB⊥平面OCC1;
(2)求二面角A-CC1-B的正弦值.
14. 某程序框图如图所示,则该程序运行后输出的值是( )
某程序框图如图所示,则该程序运行后输出的值是( )
 某程序框图如图所示,则该程序运行后输出的值是( )
某程序框图如图所示,则该程序运行后输出的值是( )| A. | 2 | B. | -3 | C. | 5 | D. | -1 |
4.曲线y=sinx+cosx在x=$\frac{π}{4}$处切线倾斜角的大小是( )
| A. | 0 | B. | $\frac{π}{4}$ | C. | -$\frac{π}{4}$ | D. | $\frac{3π}{4}$ |