题目内容
设向量
与
互相垂直，向量
与它们的夹角是60°，且|
|=5，|
|=3，|
|=8，则（
+3
）•（3
-2
）= ．
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| c |
| b |
| a |
考点：数量积表示两个向量的夹角,平面向量数量积的运算
专题：平面向量及应用
分析：根据题意，可先求出
•
、
•
与
•
的值，再计算（
+3
）•（3
-2
）．
| a |
| b |
| a |
| c |
| b |
| c |
| a |
| c |
| b |
| a |
解答：
解：根据题意，得；
•
=0，
•
=5×8•cos60°=20，
•
=3×8•cos60°=12；
∴（
+3
）•（3
-2
）=3
•
-2
2+9
•
-6
•
=0-2×52+9×12-6×20
=-62．
故答案为：-62．
| a |
| b |
| a |
| c |
| b |
| c |
∴（
| a |
| c |
| b |
| a |
| a |
| b |
| a |
| b |
| c |
| a |
| c |
=0-2×52+9×12-6×20
=-62．
故答案为：-62．
点评：本题考查了平面向量的数量积的运算问题，解题时应按照平面向量数量积的运算法则进行计算，是基础题．
练习册系列答案
相关题目
已知函数f（x+1）是偶函数，当x∈（-∞，1）时，函数f（x）单调递减，设a=f（-
），b=f（-1），c=f（2），a=f（-
），b=f（-1），c=f（2），则a，b，c的大小关系为 ．
| 1 |
| 2 |
| 1 |
| 2 |
方程x3-x-3=0的实数解所在的区间是（ ）
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |
以（-4，0）、（4，0）为焦点，2a=4的双曲线的标准方程是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
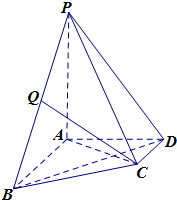如图，在四棱锥P-ABCD中，AB∥CD，AB⊥AD，AB=4，AD=2