题目内容
如图,在矩形ABCD中,AB=3
,BC=
,沿对角线BD将△BCD折起,使点C移到P点,且P在平面ABD上的射影O恰好在AB上.
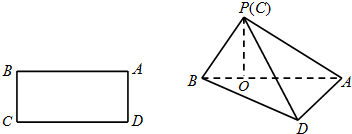
(1)求证:PB⊥PA;
(2)求点A到平面PBD的距离.
| 3 |
| 3 |

(1)求证:PB⊥PA;
(2)求点A到平面PBD的距离.
考点:点、线、面间的距离计算
专题:综合题,空间位置关系与距离
分析:(1)证明DA⊥平面PAB,PB⊥平面PAD,即可证明PB⊥PA;
(2)利用等体积转换,即可求点A到平面PBD的距离.
(2)利用等体积转换,即可求点A到平面PBD的距离.
解答:
(1)证明:由题意可得,PO⊥平面ABD
∵DA?平面ABD,
∴PO⊥DA,
由题意可知,∠DAB=90°,即DA⊥AB,且PO∩AB=O,
∴DA⊥平面PAB,又BP?平面PAB,
∴DA⊥BP,
∵PB⊥PD,DA∩PD=D,
∴PB⊥平面PAD,
∴PA?平面PAD,
∴PB⊥PA;
(2)解:设点A到平面PBD的距离为h,则
△PBA中,AB=3
,PC=BC=
,∴PO=
,
∵S△PBA=
×3
×
=3
,S△PBD=
×3
×
=
,
∴由等体积可得
•
h=
•3
•
,
∴h=
.
∵DA?平面ABD,
∴PO⊥DA,
由题意可知,∠DAB=90°,即DA⊥AB,且PO∩AB=O,
∴DA⊥平面PAB,又BP?平面PAB,
∴DA⊥BP,
∵PB⊥PD,DA∩PD=D,
∴PB⊥平面PAD,
∴PA?平面PAD,
∴PB⊥PA;
(2)解:设点A到平面PBD的距离为h,则
△PBA中,AB=3
| 3 |
| 3 |
2
| ||
| 3 |
∵S△PBA=
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 9 |
| 2 |
∴由等体积可得
| 1 |
| 3 |
| 9 |
| 2 |
| 1 |
| 3 |
| 2 |
2
| ||
| 3 |
∴h=
8
| ||
| 9 |
点评:本题考查点、线、面间的距离计算,考查线面垂直的判定与性质,考查学生分析解决问题的能力,属于中等题.

练习册系列答案
相关题目