题目内容
已知直线l:
(t为参数,θ∈R),曲线C:
(t为参数).
(1)若l与C有公共点,求直线l的斜率的取值范围;
(2)若l与C有两个公共点,求直线l的斜率的取值范围.
|
|
(1)若l与C有公共点,求直线l的斜率的取值范围;
(2)若l与C有两个公共点,求直线l的斜率的取值范围.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:直线l是表示过定点(
+1,-1),倾斜角为θ的直线;
曲线C是圆x2+y2=1(x、y为同号)上的两段弧
,
;
根据题意画出图形,结合图形,求出直线MA、MB、MC、MD与圆的切线斜率,比较即可得出所求直线斜率的范围.
| 2 |
曲线C是圆x2+y2=1(x、y为同号)上的两段弧
 |
| AD |
 |
| BC |
根据题意画出图形,结合图形,求出直线MA、MB、MC、MD与圆的切线斜率,比较即可得出所求直线斜率的范围.
解答:
解:(1)直线l:
(t为参数,θ∈R),
表示过定点(
+1,-1),倾斜角为θ的直线;
曲线C:
(t为参数)化为普通方程是
y=x
,即x2+y2=1(x、y为同号),是
,
;
如图所示;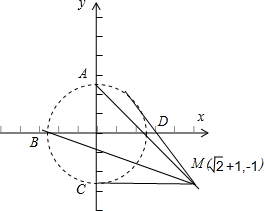
∴斜率kMC=0,kMB=
=
=-1+
;
kMA=
=-2
+2,kMD=
=-
;
设过点M的圆切线方程为y+1=k0(x-
-1),
即k0x-y-
k0-k0-1=0,
原点O到直线l的距离d=r,
即
=1,
解得k0=0,或k0=-
;
直线与曲线C相交时,直线l的斜率的取值范围是{k|-2
+2≤k≤-
,或-1+
≤k≤0};
(2)由(1)中图形知,l与C有两个公共点时,直线l的斜率的取值范围是{k|-
≤k<-
}.
|
表示过定点(
| 2 |
曲线C:
|
y=x
(
|
 |
| AD |
 |
| BC |
如图所示;

∴斜率kMC=0,kMB=
| -1 | ||
|
| ||
| 2 |
| ||
| 2 |
kMA=
| -2 | ||
|
| 2 |
| -1 | ||
|
| ||
| 2 |
设过点M的圆切线方程为y+1=k0(x-
| 2 |
即k0x-y-
| 2 |
原点O到直线l的距离d=r,
即
|-
| ||
|
解得k0=0,或k0=-
| 1 |
| 2 |
直线与曲线C相交时,直线l的斜率的取值范围是{k|-2
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(2)由(1)中图形知,l与C有两个公共点时,直线l的斜率的取值范围是{k|-
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查了直线与圆的参数方程的应用问题,解题时应把参数方程化为普通方程,并画出图形,结合图形解答问题,是中档题.

练习册系列答案
相关题目
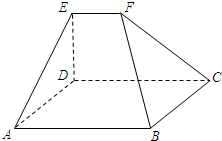 如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.
如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.