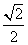题目内容
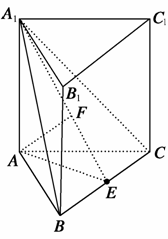
在长方体ABCD-A1B1C1D1中,AA1=AD=2,E是棱CD上的一点.
(1)求证:AD1⊥平面A1B1D;
(2)求证:B1E⊥AD1;
(3)若E是棱CD的中点,在棱AA1上是否存在点P,使得DP∥平面B1AE?若存在,求出线段AP的长;若不存在,请说明理由.
[解析] (1)证明:在长方体ABCD-A1B1C1D1中,
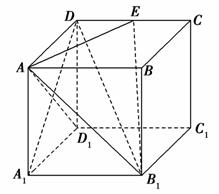
因为A1B1⊥平面A1D1DA,
所以A1B1⊥AD1.
在矩形A1D1DA中,因为AA1=AD=2,所以AD1⊥A1D.
所以AD1⊥平面A1B1D.
(2)证明:因为E∈CD,
所以B1E⊂平面A1B1CD,
由(1)可知,AD1⊥平面A1B1CD,
所以B1E⊥AD1.
(3)解:当点P是棱AA1的中点时,有DP∥平面B1AE.
理由如下:
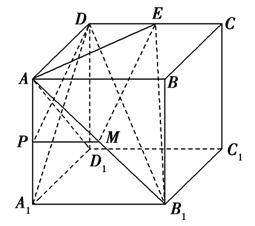
在AB1上取中点M,连接PM,ME.
因为P是棱AA1的中点,M是AB1的中点,
所以PM∥A1B1,且PM=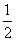 A1B1.
A1B1.
又DE∥A1B1,且DE=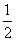 A1B1,
A1B1,
所以PM∥DE,且PM=DE,
所以四边形PMED是平行四边形,所以DP∥ME.
又DP⊄平面B1AE,ME⊂平面B1AE,
所以DP∥平面B1AE.此时,AP=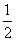 A1A=1.
A1A=1.

练习册系列答案
相关题目
 ,AA′=1,点M、N分别为A′B和B′C′的中点.
,AA′=1,点M、N分别为A′B和B′C′的中点.
 Sh,其中S为底面面积,h为高).
Sh,其中S为底面面积,h为高).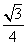 B.
B.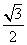
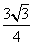 D.
D.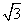
 B.1
B.1