题目内容
已知α为锐角,且sinα:sin
=3:2,则tan
的值为 .
| α |
| 2 |
| α |
| 2 |
考点:二倍角的正弦
专题:三角函数的求值
分析:由条件利用二倍角公式求得cos
的值,利用同角三角函数的基本关系可得sin
=
,从而求得tan
=
的值.
| α |
| 2 |
| α |
| 2 |
| ||
| 4 |
| α |
| 2 |
sin
| ||
cos
|
解答:
解:∵α为锐角,且sinα:sin
=3:2=2cos
,解得 cos
=
,
∴sin
=
,
则tan
=
=
,
故答案为:
.
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| 3 |
| 4 |
∴sin
| α |
| 2 |
| ||
| 4 |
则tan
| α |
| 2 |
sin
| ||
cos
|
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题主要考查二倍角公式的应用,同角三角函数的基本关系,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
设集合M={y|y=cos2x-sin2x|,x∈R},N={x||
|<1,i为虚数单位,x∈R},则M∩N为( )
| 2x | ||
1-
|
| A、(0,1) |
| B、(0,1] |
| C、[0,1) |
| D、[0,1] |
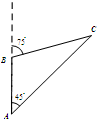 一只艘船以均匀的速度由A点向正北方向航行,如图,开始航行时,从A点观测灯塔C的方位角(从正北方向顺时针转到目标方向的水平角)为45°,行驶60海里后,船在B点观测灯塔C的方位角为75°,则A到C的距离是
一只艘船以均匀的速度由A点向正北方向航行,如图,开始航行时,从A点观测灯塔C的方位角(从正北方向顺时针转到目标方向的水平角)为45°,行驶60海里后,船在B点观测灯塔C的方位角为75°,则A到C的距离是