题目内容
在等差数列{an}中,证明
=an(n∈N*).
| a1+a2+…+a2n-1 |
| 2n-1 |
考点:等差数列的性质
专题:等差数列与等比数列
分析:
=
(a1+a2n-1)×
=an.
| a1+a2+…+a2n-1 |
| 2n-1 |
| 2n-1 |
| 2 |
| 1 |
| 2n-1 |
解答:
证明:在等差数列{an}中,
=
(a1+a2n-1)×
=
(a1+a2n-1)
=
(an+an)
=an.
∴
=an.
| a1+a2+…+a2n-1 |
| 2n-1 |
=
| 2n-1 |
| 2 |
| 1 |
| 2n-1 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=an.
∴
| a1+a2+…+a2n-1 |
| 2n-1 |
点评:本题考查等差数列的性质的灵活运用,是中档题,解题时要注意等差数列的通项公式和前n项和公式的合理运用.

练习册系列答案
相关题目
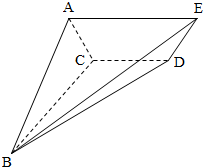 如图,四棱锥B-ACDE中,底面ACDE为直角梯形,CD∥AE,∠BCD=∠ACD=90°,二面角A-CD-B为60°,AE=BC=2,AC=CD=1.
如图,四棱锥B-ACDE中,底面ACDE为直角梯形,CD∥AE,∠BCD=∠ACD=90°,二面角A-CD-B为60°,AE=BC=2,AC=CD=1. 在直三棱柱ABC-A′B′C′中,AB⊥AC,D,E分别是BC,A′B′的中点,AB=AC=2,AA′=4.
在直三棱柱ABC-A′B′C′中,AB⊥AC,D,E分别是BC,A′B′的中点,AB=AC=2,AA′=4.