题目内容
设函数f(x)=ax2+ex(a∈R)有且仅有两个极值点x1,x2(x1<x2).
(1)求实数a的取值范围;
(2)是否存在实数a满足f(x1)=e
x1?如存在,求f(x)的极大值;如不存在,请说明理由.
(1)求实数a的取值范围;
(2)是否存在实数a满足f(x1)=e
| 2 |
| 3 |
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:(1)先求导,求出f(x)的单调性,求出参数的取值范围.
(2)根据f(x1)=e
x1,和f(x)=ax2+ex(a∈R)得到R(x)=
-
ex-e
(0<x<1),利用导数,确定函数f(x1)的单调性,从而确定最值,即可求得答案.
(2)根据f(x1)=e
| 2 |
| 3 |
| ex |
| x |
| 1 |
| 2 |
| 2 |
| 3 |
解答:
解:(1)f′(x)=2ax+ex.
显然a≠0,x1,x2是直线y=-
与曲线y=g(x)=
两交点的横坐标
由g′(x)=
=0,得x=1.列表:
此外注意到:
当x<0时,g(x)<0;
当x∈[0,1]及x∈(1,+∞)时,g(x)的取值范围分别为[0,
]和(0,
).
于是题设等价于0<-
<
⇒a<-
,故实数a的取值范围为(-∞,-
)
(2)存在实数a满足题设.证明如下:
由(1)知,0<x1<1<x2,f′(x1)=2ax1+ex1=0,
故f(x1)=ax12+ex1=ex1-
ex1=e
x1,故
-
ex1-e
=0
记R(x)=
-
ex-e
(0<x<1),则R′(x)=
-
ex<0,
于是,R(x)在(0,1)上单调递减.
又R(
)=0,故R(x)有唯一的零点x=
.
从而,满足f(x1)=e
x的x1=
.所以,a=-
e
,
此时f(x)=-
e
x2+ex,f′(x)=-
e
x+ex,
又f′(0)>0,f′(1)<0,f′(2)>0,而x1=
∈(0,1),
故当a=-
e
时,f(x)极大=f(x1)=
e
.
显然a≠0,x1,x2是直线y=-
| 1 |
| 2a |
| x |
| ex |
由g′(x)=
| 1-x |
| ex |
| x | (-∞,1) | 1 | (1,+∞) | ||
| g′(x) | + | 0 | - | ||
| g(x) | ↗ | g(x)max=
|
↘ |
当x<0时,g(x)<0;
当x∈[0,1]及x∈(1,+∞)时,g(x)的取值范围分别为[0,
| 1 |
| e |
| 1 |
| e |
于是题设等价于0<-
| 1 |
| 2a |
| 1 |
| e |
| e |
| 2 |
| e |
| 2 |
(2)存在实数a满足题设.证明如下:
由(1)知,0<x1<1<x2,f′(x1)=2ax1+ex1=0,
故f(x1)=ax12+ex1=ex1-
| x1 |
| 2 |
| 2 |
| 3 |
| ee1 |
| x1 |
| 1 |
| 2 |
| 2 |
| 3 |
记R(x)=
| ex |
| x |
| 1 |
| 2 |
| 2 |
| 3 |
| ex(x-1) |
| x2 |
| 1 |
| 2 |
于是,R(x)在(0,1)上单调递减.
又R(
| 2 |
| 3 |
| 2 |
| 3 |
从而,满足f(x1)=e
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 4 |
| 2 |
| 3 |
此时f(x)=-
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
又f′(0)>0,f′(1)<0,f′(2)>0,而x1=
| 2 |
| 3 |
故当a=-
| 3 |
| 4 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查了利用导数求函数的极值,研究函数的零点问题,利用导数研究函数的单调性,对于利用导数研究函数的单调性,注意导数的正负对应着函数的单调性.解题时要注意运用极值点必定是导函数对应方程的根,而导函数对应方程的根不一定是极值点.属于中档题.

练习册系列答案
相关题目
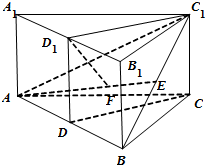 如图,已知直三棱柱ABC-A1B1C1(侧棱与底面垂直的三棱柱为直三棱柱)中,CA=CB,D,D1,E分别为边AB,A1B1,BC1的中点.
如图,已知直三棱柱ABC-A1B1C1(侧棱与底面垂直的三棱柱为直三棱柱)中,CA=CB,D,D1,E分别为边AB,A1B1,BC1的中点.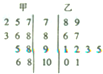 某科考试中,从甲、乙两个班级各随机抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
某科考试中,从甲、乙两个班级各随机抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.