题目内容
 如图所示,四边形PDCE为矩形,四边形ABCD为直角梯形,且∠BAD=∠ADC=90°,平面PDCE⊥平面ABCD,AB=AD=
如图所示,四边形PDCE为矩形,四边形ABCD为直角梯形,且∠BAD=∠ADC=90°,平面PDCE⊥平面ABCD,AB=AD=| 1 |
| 2 |
| 2 |
(Ⅰ)若M为PA中点,求证:AC∥平面MDE;
(Ⅱ)求该几何体被平面PBD所分成的两部分的体积比.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)M为PA中点,连结PC,交DE与N,连结MN,通过直线与平面平行的判定定理即可求证:AC∥平面MDE;
(Ⅱ)证明PD⊥平面ABD,求出VP-AED,证明AD⊥平面PDCE,求出四棱锥的体积VE-PDCE的体积即可得到比值.
(Ⅱ)证明PD⊥平面ABD,求出VP-AED,证明AD⊥平面PDCE,求出四棱锥的体积VE-PDCE的体积即可得到比值.
解答:
解:(Ⅰ)证明:连结PC,交DE与N,连结MN,
△PAC中,M,N分别为两腰PA,PC的中点,
∴MN∥AC.…(2分)
因为MN?面MDE,又AC?面MDE,
所以AC∥平面MDE.…(4分)

(Ⅱ)解:由四边形PDCE为矩形,知PD⊥DC.
又平面PDCE⊥平面ABCD,
∴PD⊥平面ABD …(6分)
三棱锥P-ABD的体积为
VP-AED=
S△AED×PD=
×
AB×AD×PD=
×1×1×
=
.…(8分)
由已知AD⊥DC,又平面PDCE⊥平面ABCD,
∴AD⊥平面PDCE,∵AB∥CD,四棱锥的体积为
VE-PDCE=
SPDCE×AD=
CD×PD×AD=
×2×
×1=
.…(10分)
=
=4,或者
=
=
,
所以原几何体被平面PBD所分成的两部分的体积比4或
.…(12分)
△PAC中,M,N分别为两腰PA,PC的中点,
∴MN∥AC.…(2分)
因为MN?面MDE,又AC?面MDE,
所以AC∥平面MDE.…(4分)

(Ⅱ)解:由四边形PDCE为矩形,知PD⊥DC.
又平面PDCE⊥平面ABCD,
∴PD⊥平面ABD …(6分)
三棱锥P-ABD的体积为
VP-AED=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| ||
| 6 |
由已知AD⊥DC,又平面PDCE⊥平面ABCD,
∴AD⊥平面PDCE,∵AB∥CD,四棱锥的体积为
VE-PDCE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
2
| ||
| 3 |
| VE-PDCE |
| VP-AED |
| ||||
|
| VP-AED |
| VE-PDCE |
| ||||
|
| 1 |
| 4 |
所以原几何体被平面PBD所分成的两部分的体积比4或
| 1 |
| 4 |
点评:本题考查直线与平面的平行的判定定理以及直线与平面垂直的判定定理的应用,几何体的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
数列{an}中,an+1=
,已知该数列既是等差数列又是等比数列,则该数列的前20项的和等于( )
| an2 |
| 2an-5 |
| A、100 |
| B、0或100 |
| C、100或-100 |
| D、0或-100 |
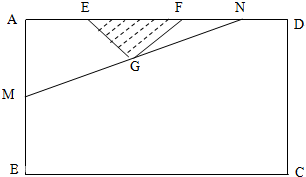 某小区想利用一矩形空地ABCD建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场,设DN=x(m)
某小区想利用一矩形空地ABCD建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场,设DN=x(m)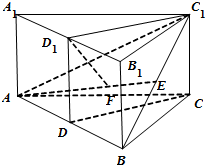 如图,已知直三棱柱ABC-A1B1C1(侧棱与底面垂直的三棱柱为直三棱柱)中,CA=CB,D,D1,E分别为边AB,A1B1,BC1的中点.
如图,已知直三棱柱ABC-A1B1C1(侧棱与底面垂直的三棱柱为直三棱柱)中,CA=CB,D,D1,E分别为边AB,A1B1,BC1的中点.