题目内容

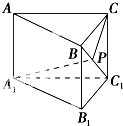如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=6，BC=CC1=
2
，P是BC1上一动点，则|CP|+|PA1|的最小值是
 
．
考点：多面体和旋转体表面上的最短距离问题
专题：计算题,空间位置关系与距离
分析：沿BC1将△CBC1展开与△A1BC1在同一个平面内，不难看出CP+PA1的最小值是A1C的连线．
解答： 解：由题意，△A1C1B是直角三角形，沿BC1展开，△CC1B是等腰直角三角形，
作CE⊥A1C1，CE=C1E=1，
∴|CP|+|PA1|=|A1C|=
72+12
=5
2
．
故答案为：5
2
．
点评：本题考查棱柱的结构特征及两点之间的距离，其中将△CBC1沿BC1展开，将一个空间问题转化为平面内求两点之间距离问题是解答本题的关键．
练习册系列答案
相关题目
设非零数列{an}满足anan+2=an+12+λ（-1）n+1（n∈N+）．
（1）当λ=0时，求证：an-man+m=an2，（n＞m 且m，n∈R+）．
（2）当a1=1，a2=2，λ=3，求证：an+2=an+3an+1．
已知三点A，B，C的坐标分别为A（1，0），B（0，-1），C（cosa，sina），其中a∈（0，π）．
（1）若|
AC
|=|
BC
|，求角a的值．
（2）若
AC
•
BC
=
2
3
，求
2sin2a+sin2a
1+tana
的值．
设直线nx+（n+1）y=
2
（n∈N*）与两坐标轴围成的三角形的面积为Sn，则S1+S2+S3+…+S2013的值为
 
．
若函数y=sin（2x+φ）为偶函数，则φ的一个值可以是
 
．
在平面直角坐标系xOy中，D是到原点的距离不大于1的点构成的区域，E是满足不等式组
x-y+1≥0
x+y≥0
x≤0
的点（x，y）构成的区域，向D中随机投一点，则所投的点落在E中的概率是
 
．
已知函数f（x）=sin（x+θ）+cos（x+θ）是偶函数，且θ∈[0，
π
2
]，则θ的值为
 
．
已知复数（1+i）•（1-bi）为实数，则实数b的值为
 
．
设函数f（x）=x2-12x+b，则下列结论正确的是（　　）
A、函数f（x）在（-∞，-1）上单调递增
B、函数f（x）在（-∞，-1）上单调递减
C、若b=-6，则函数f（x）的图象在点（-2，f（-2））处的切线方程为y=10
D、若b=0，则函数f（x）的图象与直线y=10只有一个公共点

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网