题目内容
已知三点A，B，C的坐标分别为A（1，0），B（0，-1），C（cosa，sina），其中a∈（0，π）．
（1）若|
|=|
|，求角a的值．
（2）若
•
=
，求
的值．
（1）若|
| AC |
| BC |
（2）若
| AC |
| BC |
| 2 |
| 3 |
| 2sin2a+sin2a |
| 1+tana |
考点：平面向量数量积的运算,同角三角函数基本关系的运用
专题：平面向量及应用
分析：（1）
=(cosα-1，sinα)，
=(cosα，sinα+1)，由|
|=|
|，推导出sinα=cosα，由此能求出α=
．
（2）由
•
=
，推导出cosα-sinα=
，从而得到2sinαcosα=
，再由
=
，能求出结果．
| AC |
| BC |
| AC |
| BC |
| π |
| 4 |
（2）由
| AC |
| BC |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 9 |
| 2sin2a+sin2a |
| 1+tana |
| 2sinα(sinα+cosα) | ||
|
解答：
解：（1）∵A（1，0），B（0，-1），C（cosa，sina），a∈（0，π）．
∴
=(cosα-1，sinα)，
=(cosα，sinα+1)，
∵|
|=|
|，
∴（cosα-1）2+sin2α=cos2α+（sinα+1）2，
整理，得sinα=cosα，
∵a∈（0，π），∴α=
．
（2）∵
•
=
，
∴cosα•（cosα-1）+sinα•（sinα+1）
=cos2α-cosα+sin2α+sinα
=1-cosα+sinα=
，
∴cosα-sinα=
，
∴1-2sinαcosα=
，∴2sinαcosα=
，
∴
=
=2sinαcosα=
．
∴
| AC |
| BC |
∵|
| AC |
| BC |
∴（cosα-1）2+sin2α=cos2α+（sinα+1）2，
整理，得sinα=cosα，
∵a∈（0，π），∴α=
| π |
| 4 |
（2）∵
| AC |
| BC |
| 2 |
| 3 |
∴cosα•（cosα-1）+sinα•（sinα+1）
=cos2α-cosα+sin2α+sinα
=1-cosα+sinα=
| 2 |
| 3 |
∴cosα-sinα=
| 1 |
| 3 |
∴1-2sinαcosα=
| 1 |
| 9 |
| 8 |
| 9 |
∴
| 2sin2a+sin2a |
| 1+tana |
| 2sinα(sinα+cosα) | ||
|
=2sinαcosα=
| 8 |
| 9 |
点评：本题考查角的大小的求法，考查三角函数值的求法，是中档题，解题时要认真审题，注意平面向量知识的灵活运用．
练习册系列答案
名校课堂系列答案
相关题目
已知等差数列{an}的前n项和为Sn，已知a5=9，S10=100
（1）求数列{an}的通项公式；
（2）记数列{
}的前n项和为Tn，数列{
}的前n项和为Un，求证：Un＜2．
（1）求数列{an}的通项公式；
（2）记数列{
| Sn |
| n |
| 1 |
| Sn+1-Tn+1 |
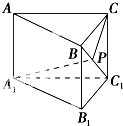如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=6，BC=CC1=