题目内容
在平面直角坐标系xOy中,D是到原点的距离不大于1的点构成的区域,E是满足不等式组
的点(x,y)构成的区域,向D中随机投一点,则所投的点落在E中的概率是 .
|
考点:几何概型,二元一次不等式(组)与平面区域
专题:概率与统计
分析:求出对应区域的面积,利用几何概型的概率公式即可得到结论.
解答:
 解:区域D对应的平面区域为半径为1的圆,面积为S=π,
解:区域D对应的平面区域为半径为1的圆,面积为S=π,
区域E对应的区域为三角形AOC,
由
,解得
,即C(-
,
),
A(0,1),
则三角形AOC的面积S=
×1×
=
,
则对应的概率为
=
,
故答案为:
.
 解:区域D对应的平面区域为半径为1的圆,面积为S=π,
解:区域D对应的平面区域为半径为1的圆,面积为S=π,区域E对应的区域为三角形AOC,
由
|
|
| 1 |
| 2 |
| 1 |
| 2 |
A(0,1),
则三角形AOC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
则对应的概率为
| ||
| π |
| 1 |
| 4π |
故答案为:
| 1 |
| 4π |
点评:本题主要考查几何概型的概率的计算,根据条件,求出对应区域的面积是解决本题的关键.

练习册系列答案
相关题目
?α∈(
,
),x=(sinα)logπcosα,y=(cosα)logπsinα,则x与y的大小关系为( )
| π |
| 4 |
| π |
| 2 |
| A、x>y | B、x<y |
| C、x=y | D、不确定 |
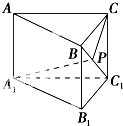 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=6,BC=CC1=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=6,BC=CC1=