题目内容
若函数y=sin(2x+φ)为偶函数,则φ的一个值可以是 .
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由条件根据正弦函数、余弦函数的奇偶性可得 φ=kπ+
,k∈Z,从而得出结论.
| π |
| 2 |
解答:
解:∵函数y=sin(2x+φ)为偶函数,∴φ=kπ+
,k∈Z,
故可取φ=
,
故答案为:
.
| π |
| 2 |
故可取φ=
| π |
| 2 |
故答案为:
| π |
| 2 |
点评:本题主要考查正弦函数、余弦函数的奇偶性,属于基础题.

练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn,已知a5=9,S10=100
(1)求数列{an}的通项公式;
(2)记数列{
}的前n项和为Tn,数列{
}的前n项和为Un,求证:Un<2.
(1)求数列{an}的通项公式;
(2)记数列{
| Sn |
| n |
| 1 |
| Sn+1-Tn+1 |
长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E和F分别是A1B1和C1D1的中点,求:
(1)找出与AB1异面的所有棱;
(2)AC和B1C1所成角的余弦值;
(3)EB和FD所成角.
(1)找出与AB1异面的所有棱;
(2)AC和B1C1所成角的余弦值;
(3)EB和FD所成角.
已知数列{an}的前n项之和Sn=n2-4n+1,则|a1|+|a2|+…+|a10|的值为( )
| A、61 | B、65 | C、67 | D、68 |
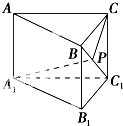 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=6,BC=CC1=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=6,BC=CC1=