题目内容
设函数f(x)=x2-12x+b,则下列结论正确的是( )
| A、函数f(x)在(-∞,-1)上单调递增 |
| B、函数f(x)在(-∞,-1)上单调递减 |
| C、若b=-6,则函数f(x)的图象在点(-2,f(-2))处的切线方程为y=10 |
| D、若b=0,则函数f(x)的图象与直线y=10只有一个公共点 |
考点:二次函数的性质
专题:导数的概念及应用
分析:利用二次函数的性质,求函数在某一点的切线方程的方法,判断各个选项是否正确,从而得出结论.
解答:
解:由于函数f(x)=x2-12x+b的对称轴为x=6,故函数f(x)在(-∞,6)上单调递减,
故A不正确,B正确.
若b=-6,由于点(-2,f(-2))即点(-2,22),f′(-2)=-16,
故函数f(x)的图象在点(-2,f(-2))处的切线方程为y-22=-16(x+2),故C不正确.
若b=0,则函数f(x)=x2-12x=(x-6)2-36的图象与直线y=10有两个公共点,故D不正确,
故选:B.
在函数f(x)在(-∞,-1)上单调递
故A不正确,B正确.
若b=-6,由于点(-2,f(-2))即点(-2,22),f′(-2)=-16,
故函数f(x)的图象在点(-2,f(-2))处的切线方程为y-22=-16(x+2),故C不正确.
若b=0,则函数f(x)=x2-12x=(x-6)2-36的图象与直线y=10有两个公共点,故D不正确,
故选:B.
在函数f(x)在(-∞,-1)上单调递
点评:本题主要考查二次函数的性质,求函数在某一点的切线方程的方法,属于基础题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
已知数列{an}的前n项之和Sn=n2-4n+1,则|a1|+|a2|+…+|a10|的值为( )
| A、61 | B、65 | C、67 | D、68 |
?α∈(
,
),x=(sinα)logπcosα,y=(cosα)logπsinα,则x与y的大小关系为( )
| π |
| 4 |
| π |
| 2 |
| A、x>y | B、x<y |
| C、x=y | D、不确定 |
△ABC的内角A、B、C所对的边分别为a,b,c,若三边的长为连续的三个正整数,且A>B>C,9b=10acosC,则sinA:sinB:sinC为( )
| A、4:3:2 |
| B、5:6:7 |
| C、5:4:3 |
| D、6:5:4 |
南宁市十二路公共汽车每5分钟一趟,某位同学每天乘十二路公共汽车上学,则他等车时间小于3分钟的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=2sin2x(x∈R)是( )
| A、偶函数 |
| B、奇函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数又不是偶函数 |
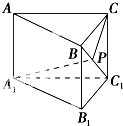 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=6,BC=CC1=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=6,BC=CC1=