题目内容
设直线nx+(n+1)y=
(n∈N*)与两坐标轴围成的三角形的面积为Sn,则S1+S2+S3+…+S2013的值为 .
| 2 |
考点:数列的求和
专题:计算题,规律型
分析:分别求出直线nx+(n+1)y=
(n∈N*)与两坐标轴的交点,即(
,0),(0,
),则Sn=
=
-
,然后分别代入1,2,…,2013,最后求和即可.
| 2 |
| ||
| n |
| ||
| n+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:分别令x=0和y=0,得到直线nx+(n+1)y=
(n∈N*)与两坐标轴的交点:
(
,0),(0,
),
则Sn=
•
•
=
=
-
,
然后分别代入1,2,…,2013,
则有S1+S2+S3+…+S2013=1-
+
-
+
-
+…+
-
=1-
=
.
故答案为:
.
| 2 |
(
| ||
| n |
| ||
| n+1 |
则Sn=
| 1 |
| 2 |
| ||
| n |
| ||
| n+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
然后分别代入1,2,…,2013,
则有S1+S2+S3+…+S2013=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2013 |
| 1 |
| 2014 |
=1-
| 1 |
| 2014 |
| 2013 |
| 2014 |
故答案为:
| 2013 |
| 2014 |
点评:本题主要考查数列的求和方法:裂项相消法.要求会求一次函数与两坐标轴的交点坐标;熟悉三角形的面积公式;记住:
=
-
(n为自然数)是解题的关键.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |

练习册系列答案
相关题目
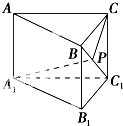 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=6,BC=CC1=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=6,BC=CC1=