题目内容
19.对于正整数n,设曲线y=xn(2-x)在x=2处的切线与y轴交点的纵坐标为an,则数列{an}的前n项和为Sn=2n+2-4.分析 利用导数的几何意义求出切线方程为y=-2n(x-2),从而得到an=2n+1,利用等比数列的求和公式能求出Sn.
解答 解:∵y=xn(2-x),∴y'=2nxn-1-(n+1)xn,
∴曲线y=xn(2-x)在x=2处的切线的斜率为k=n2n-(n+1)2n=-2n,
切点为(2,0),
∴切线方程为y=-2n(x-2),
令x=0得an=2n+1,
∴Sn=$\frac{4(1-{2}^{n})}{1-2}$=2n+2-4,
故答案为:2n+2-4.
点评 考查学生利用导数研究曲线上某点切线方程的能力,以及利用等比数列的求和公式进行数列求和的能力.

练习册系列答案
相关题目
10.“x≤2或x≥5”是“x2-7x+10>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.“m>0”是“x2+x+m=0无实根”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.某学校为了解三年级、六年级、九年级这三个年级学生的视力情况,拟从中抽取一定比例的学生进行调杳,则最合理的抽样方法是( )
| A. | 抽签法 | B. | 系统抽样法 | C. | 分层抽样法 | D. | 随机数法 |
9.函数f(x)=3sin(2x-$\frac{π}{3}$)的图象的一条对称轴是( )
| A. | $x=\frac{π}{3}$ | B. | $x=\frac{5π}{12}$ | C. | $x=\frac{π}{2}$ | D. | $x=\frac{5π}{6}$ |
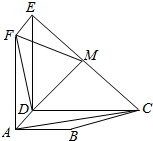 如图,四边形ABCD是梯形,AB∥CD,∠ADC=90°,四边形ADEF是矩形,且平面
如图,四边形ABCD是梯形,AB∥CD,∠ADC=90°,四边形ADEF是矩形,且平面