题目内容
2.在△ABC中,角A,B,C的对边是a,b,c,若asinA=csinC,b2+ac=a2+c2,则a,b,c等于( )| A. | 1:1:2 | B. | 1:$\sqrt{2}$:1 | C. | 1:1:1 | D. | 1:1:$\sqrt{2}$ |
分析 b2+ac=a2+c2,利用余弦定理可得cosB=$\frac{1}{2}$,B∈(0,π),可得B.由asinA=csinC,利用正弦定理可得:a=c.即可得出三角形的形状.
解答 解:∵b2+ac=a2+c2,∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{1}{2}$,B∈(0,π),∴$B=\frac{π}{3}$.
∵asinA=csinC,利用正弦定理可得:a2=c2,可得a=c.
∴△ABC是等边三角形,
∴a:b:c=1:1:1.
故选:C.
点评 本题考查了正弦定理余弦定理、等边三角形的判定,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.“x≤2或x≥5”是“x2-7x+10>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.设a=20.4,b=30.75,c=log3$\frac{1}{3}$,则( )
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | b>c>a |
11.某学校为了解三年级、六年级、九年级这三个年级学生的视力情况,拟从中抽取一定比例的学生进行调杳,则最合理的抽样方法是( )
| A. | 抽签法 | B. | 系统抽样法 | C. | 分层抽样法 | D. | 随机数法 |
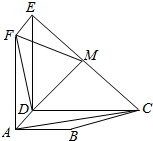 如图,四边形ABCD是梯形,AB∥CD,∠ADC=90°,四边形ADEF是矩形,且平面
如图,四边形ABCD是梯形,AB∥CD,∠ADC=90°,四边形ADEF是矩形,且平面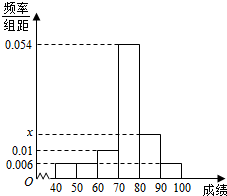 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( )
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( )