题目内容
若方程
+
=1表示椭圆，则实数m的取值范围 ．
| x2 |
| 3-m |
| y2 |
| m-1 |
考点：椭圆的标准方程
专题：圆锥曲线的定义、性质与方程
分析：由椭圆的性质得
，由此能求出实数m的取值范围．
|
解答：
解：∵方程
+
=1表示椭圆，
∴
，
解得1＜m＜3，且m≠2，
∴实数m的取值范围是（1，2）∪（2，3）．
故答案为：（1，2）∪（2，3）．
| x2 |
| 3-m |
| y2 |
| m-1 |
∴
|
解得1＜m＜3，且m≠2，
∴实数m的取值范围是（1，2）∪（2，3）．
故答案为：（1，2）∪（2，3）．
点评：本题考查实数的取值范围的求法，是基础题，解题时要认真审题，注意椭圆性质的合理运用．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
等比数列{an}的前n项和为Sn（n∈N*），若a3=
，S3=
，则此数列的首项为（ ）
| 3 |
| 2 |
| 9 |
| 2 |
| A、6 | ||
B、-
| ||
C、
| ||
D、
|
a为如图所示的程序框图中输出的结果，则a的值是如图是导函数y=f′（x）的图象，则下列命题错误的是（ ）
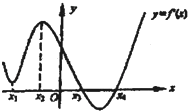
| A、导函数y=f′（x）在x1处有极小值 |
| B、导函数y=f′（x）在x2处有极大值 |
| C、导函数y=f（x）在x3处有极小值 |
| D、导函数y=f（x）在x4处有极小值 |