题目内容
已知二次函数f(x)满足f(1)=0,且f(x+1)-f(x)=4x+3.
(1)求f(x)的解析式,
(2)若f(x)在区间[a,a+1]上单调,求实数a的取值范围.
(1)求f(x)的解析式,
(2)若f(x)在区间[a,a+1]上单调,求实数a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)设出f(x)的解析式,根据f(1)=0,且f(x+1)-f(x)=4x+3构造系数的方程组,解得函数的解析式;
(2)根据(1)中函数的解析式,分析出函数的单调性,进而结合f(x)在区间[a,a+1]上单调,可得实数a的取值范围.
(2)根据(1)中函数的解析式,分析出函数的单调性,进而结合f(x)在区间[a,a+1]上单调,可得实数a的取值范围.
解答:
解:(1)设y=f(x)=ax2+bx+c,
∵f(1)=0且f(x+1)-f(x)=4x+3,
∴a+b+c=0且a(x+1)2+b(x+1)+c-(ax2+bx+c)=4x+3,
∴2a=4,a+b=3,
解得a=2,b=1,c=-3,
函数f(x)的表达式为f(x)=2x2+x-3,
(2)∵f(x)=2x2+x-3的图象是开口朝上且以直线x=-
为对称轴的抛物线,
若f(x)在区间[a,a+1]上单调,
则a≥-
,或a+1≤-
,
∴a≥-
,或a≤-
.
∵f(1)=0且f(x+1)-f(x)=4x+3,
∴a+b+c=0且a(x+1)2+b(x+1)+c-(ax2+bx+c)=4x+3,
∴2a=4,a+b=3,
解得a=2,b=1,c=-3,
函数f(x)的表达式为f(x)=2x2+x-3,
(2)∵f(x)=2x2+x-3的图象是开口朝上且以直线x=-
| 1 |
| 4 |
若f(x)在区间[a,a+1]上单调,
则a≥-
| 1 |
| 4 |
| 1 |
| 4 |
∴a≥-
| 1 |
| 4 |
| 5 |
| 4 |
点评:本题考查利用待定系数法求函数的解析式,二次函数的图象和性质,属于基础题,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
直线y=kx+b在坐标系中的位置如图,则( )
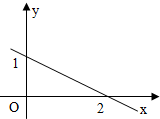

A、k=-
| ||
B、k=-
| ||
C、k=
| ||
D、k=
|
如果函数f(x)=x2-2bx+2在区间[3,+∞)上是增函数,则b的取值范围为( )
| A、b=3 | B、b≥3 |
| C、b≤3 | D、b≠3 |