题目内容
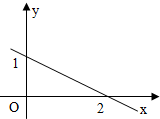
直线y=kx+b在坐标系中的位置如图，则（ ）
A、k=-
| ||
B、k=-
| ||
C、k=
| ||
D、k=
|
考点：直线的斜截式方程
专题：直线与圆
分析：由截距的意义可得b值，由斜率公式可得k值，可得答案．
解答：
解：由图象和截距的意义可得b=1，
由直线过点（0，1）和（2，0）和斜率公式可得：k=
=-
，
故选：B
由直线过点（0，1）和（2，0）和斜率公式可得：k=
| 1-0 |
| 0-2 |
| 1 |
| 2 |
故选：B
点评：本题考查直线的斜截式方程和几何意义，属基础题．
练习册系列答案
相关题目
已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2-6x已知命题p：若a＞b，则a2＞b2；命题q：若a＜b，则a+c＜b+c，下列命题为真的是（ ）
| A、p∧q | B、p∧（?q） |
| C、p∨（?q） | D、p∨q |
下列关系正确的是（ ）
| A、0∈N | B、1⊆R |
| C、{π}⊆Q | D、-3∉Z |