Question

抛物线y=x²与直线x+y=2所围图形的面积

 

．

Answer 1

考点：定积分在求面积中的应用

专题：函数的性质及应用

分析：由

y=x2 y=2-x

得x²+x-2=0，解得：x=-2，x=1，依题意，二曲线所围成的图形的面积S=

∫

1 -2

[（2-x）-x²]dx，利用微积分定理可得答案．

解答： 解：由

y=x2 y=2-x

得x²+x-2=0，解得：x=-2，x=1，
故积分区间[-2，1]，
当x∈[-2，1]时，直线x+y=2在抛物线y=x²的上方，

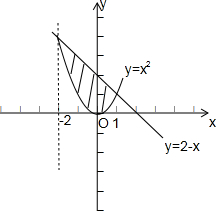
故抛物线y=x²与直线x+y=2所围成的图形的面积
S=

∫

1 -2

[（2-x）-x²]dx
=（2x-

1

2

x²-

1

3

x³）

|

1 -2

=（2×1-

1

2

×1²-

1

3

×1³）-[2×（-2）-

1

2

×（-2）²-

1

3

（-2）³]
=

9

2

．
故答案为：

9

2

．

点评：本题考查定积分在求面积中的应用，得到抛物线y=x²与直线x+y=2所围成的图形的面积S=

∫

1 -2

[（2-x）-x²]dx是关键，考查等价转化思想与运算求解能力，属于中档题．