题目内容
18.在△ABC中,若$\frac{a}{sinA}$=6,B=$\frac{π}{3}$,a+c=6,则△ABC的面积为$\frac{3\sqrt{3}}{4}$.分析 由正弦定理解出b,利用余弦定理解出ac,代入三角形的面积公式求出面积.
解答 解:在△ABC中,由正弦定理得$\frac{b}{sinB}=\frac{a}{sinA}=6$,∴b=6sinB=3$\sqrt{3}$.
由余弦定理得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}=\frac{(a+c)^{2}-2ac-{b}^{2}}{2ac}$=$\frac{9-2ac}{2ac}=\frac{1}{2}$,
解得ac=3,
∴S=$\frac{1}{2}acsinB$=$\frac{1}{2}×3×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$.\
故答案为:$\frac{3\sqrt{3}}{4}$.
点评 本题考查了正弦定理与余弦定理在解三角形中的应用,属于中档题.

练习册系列答案
相关题目
6.已知实数对(x,y),设映射f:(x,y)→($\frac{x+y}{2}$,$\frac{x-y}{2}$),并定义|(x,y)|=$\sqrt{{x}^{2}{+y}^{2}}$,若|f[f(f(x,y))]|=8,则|(x,y)|的值为( )
| A. | 4$\sqrt{2}$ | B. | 8$\sqrt{2}$ | C. | 16$\sqrt{2}$ | D. | 32$\sqrt{2}$ |
13.已知不等式组$\left\{\begin{array}{l}{x+y≤1}\\{x-y≥-1}\\{y≥0}\end{array}\right.$所表示的平面区域为D,直线l:y=3x+m不经过区域D,则实数m的取值范围是( )
| A. | [-3,1] | B. | [-3,3] | C. | (-∞,-3)∪(1,+∞) | D. | (-∞,-3)∪(3,+∞) |
5.如图是某个四面体的三视图,则该四面体的表面积为( )
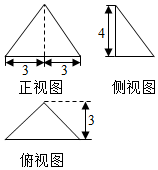

| A. | 12+24$\sqrt{2}$ | B. | 24+24$\sqrt{2}$ | C. | 12+12$\sqrt{2}$ | D. | 24+12$\sqrt{2}$ |
2.已知函数f(x)=$\left\{\begin{array}{l}-{x^2}+3x,x<0\\ ln(x+1),x≥0\end{array}\right.$,若|f(x)|≥ax,则a的取值范围是( )
| A. | (-∞,0] | B. | (-∞,1] | C. | [-3,0] | D. | [-3,1] |
3.执行如图所示的程序框图,则输出的S为( )


| A. | 2 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{2}$ | D. | -3 |