题目内容
6.已知实数对(x,y),设映射f:(x,y)→($\frac{x+y}{2}$,$\frac{x-y}{2}$),并定义|(x,y)|=$\sqrt{{x}^{2}{+y}^{2}}$,若|f[f(f(x,y))]|=8,则|(x,y)|的值为( )| A. | 4$\sqrt{2}$ | B. | 8$\sqrt{2}$ | C. | 16$\sqrt{2}$ | D. | 32$\sqrt{2}$ |
分析 根据新定义得出|f[f(f(x,y))]|=8,|($\frac{x+y}{4}$,$\frac{x-y}{4}$)|=8,计算即可.
解答 解:∵映射f:(x,y)→($\frac{x+y}{2}$,$\frac{x-y}{2}$),
∴f[f(f(x,y))]=f(f($\frac{x+y}{2}$,$\frac{x-y}{2}$))=f($\frac{x}{2}$,$\frac{y}{2}$)=($\frac{x+y}{4}$,$\frac{x-y}{4}$),
∵定义|(x,y)|=$\sqrt{{x}^{2}{+y}^{2}}$,若|f[f(f(x,y))]|=8,
∴|($\frac{x+y}{4}$,$\frac{x-y}{4}$)|=8,
∴$\sqrt{(\frac{x+y}{4})^{2}+(\frac{x-y}{4})^{2}}$=8,
$\sqrt{{x}^{2}+{y}^{2}}=16\sqrt{2}$
∴|(x,y)|的值为16$\sqrt{2}$,
故选:C
点评 本题考察了映射的概念,关键是理解题目条件的含义,展开计算即可,属于中档题目.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
14.命题甲:α=30°,命题乙:sin$α=\frac{1}{2}$,则命题甲是命题乙成立的( )
| A. | 充分条件而非必要条件 | B. | 必要条件而非充分条件 | ||
| C. | 充要条件 | D. | 非充分条件也非必要条件 |
10.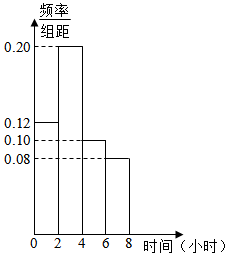 研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是( )
研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是( )
 研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是( )
研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是( )| A. | 1.78小时 | B. | 2.24小时 | C. | 3.56小时 | D. | 4.32小时 |
11.将函数y=cos(2x+$\frac{π}{3}$)的图象向左平移$\frac{π}{6}$个单位,得到函数y=f(x)的图象,则下列说法正确的是( )
| A. | f(x)是偶函数 | B. | f(x)周期为$\frac{π}{2}$ | ||
| C. | f(x)图象关于x=$\frac{π}{6}$对称 | D. | f(x)图象关于(-$\frac{π}{6}$,0)对称 |