题目内容
5．如图是某个四面体的三视图，则该四面体的表面积为（ ）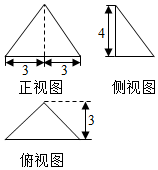
| A． | 12+24$\sqrt{2}$ | B． | 24+24$\sqrt{2}$ | C． | 12+12$\sqrt{2}$ | D． | 24+12$\sqrt{2}$ |
分析 由已知中的三视图可得该几何体是一个以俯视图为底面的三棱锥，计算出各个面的面积，可得答案．
解答 解：由已知中的三视图可得该几何体是一个以俯视图为底面的三棱锥，
底面面积为：$\frac{1}{2}×6×3$=9，
前侧面面积为：$\frac{1}{2}×6×\sqrt{{3}^{2}+{4}^{2}}$=15，
左右两个侧面的面积均为：$\frac{1}{2}×3\sqrt{2}×4$=6$\sqrt{2}$，
故该四面体的表面积为：24+12$\sqrt{2}$，
故选：D．
点评 本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键．
练习册系列答案
相关题目
5．已知平面向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（m，n），且2$\overrightarrow{a}$=$\overrightarrow{b}$，则2$\overrightarrow{a}$-3$\overrightarrow{b}$等于（ ）
| A． | （-2，-4） | B． | （-3，-6） | C． | （-5，-10） | D． | （-4，-8） |
10．
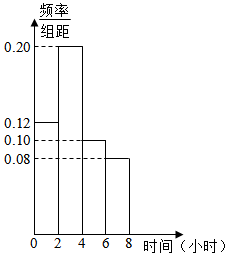研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间，并将其绘制为如图所示的频率分布直方图．若同一组数据用该区间的中点值作代表，则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是（ ）
研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间，并将其绘制为如图所示的频率分布直方图．若同一组数据用该区间的中点值作代表，则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是（ ）| A． | 1.78小时 | B． | 2.24小时 | C． | 3.56小时 | D． | 4.32小时 |
14．在△ABC中，角A，B，C的对边分别为a，b，c，若$sinA=2sinB，cosC=-\frac{1}{4}$，则$\frac{c}{a}$=（ ）
| A． | $\sqrt{6}$ | B． | $\frac{{\sqrt{6}}}{2}$ | C． | $\sqrt{3}$ | D． | $\frac{{\sqrt{3}}}{2}$ |