题目内容

3．集合A={（x，y）||x|≤1，|y|≤1}，B={（x，y）|（x-a）2+（y-a）2≤1}，若集合A∩B=∅，则实数a的取值范围是（-∞，-1-$\frac{\sqrt{2}}{2}$]]∪[1+$\frac{\sqrt{2}}{2}$，+∞）．．

分析 由题意画出图形，数形结合可得使A∩B=∅的实数a的取值范围．

解答 解：A={（x，y）||x|≤1，|y|≤1}，B={（x，y）|（x-a）2+（y-a）2＜1}，
如图，|ON|=$\sqrt{2}$+1，则|OM|=1+$\frac{\sqrt{2}}{2}$，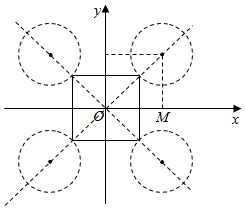

要使A∩B=∅，则a≥1+$\frac{\sqrt{2}}{2}$或a≤-1-$\frac{\sqrt{2}}{2}$．
故答案为：（-∞，-1-$\frac{\sqrt{2}}{2}$]]∪[1+$\frac{\sqrt{2}}{2}$，+∞）．

点评 本题主要考查二元一次不等式（组）与平面区域、集合关系中的参数取值问题、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想，属于中档题．

练习册系列答案
相关题目
13．（x-2y）（x+y）5的展开式中x3y3的系数为（　　）
A．-10B．-20C．30D．10
14．命题甲：α=30°，命题乙：sin$α=\frac{1}{2}$，则命题甲是命题乙成立的（　　）
A．充分条件而非必要条件B．必要条件而非充分条件
C．充要条件D．非充分条件也非必要条件
11．将函数f（x）=sin（2x+$\frac{π}{6}$）的图象向左平移φ（0＜φ＜$\frac{π}{2}$）个单位得到y=g（x）的图象，|f（x1）-g（x2）|=2的x1，x2，|x1-x2|min=$\frac{π}{4}$，则φ的值是$\frac{π}{4}$．
18．在△ABC中，若$\frac{a}{sinA}$=6，B=$\frac{π}{3}$，a+c=6，则△ABC的面积为$\frac{3\sqrt{3}}{4}$．
3．（题类A）双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0），过焦点F1的弦AB长为m（A，B在同一支上），另一个焦点为F2，则△ABF2的周长为（　　）
A．4a-2mB．4aC．4a+mD．4a+2m
10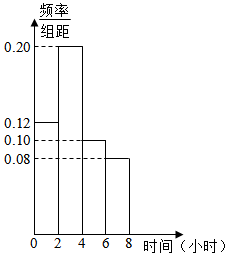．研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间，并将其绘制为如图所示的频率分布直方图．若同一组数据用该区间的中点值作代表，则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是（　　）
A．1.78小时B．2.24小时C．3.56小时D．4.32小时
7．已知函数f（x）=Asin（2x+φ）（A＞0），其中角φ的终边经过点P（-l，1），且0＜φ＜π．则φ=$\frac{3π}{4}$，f（x）的单调减区间为[-$\frac{π}{8}$+kπ，$\frac{3π}{8}$+kπ]（k∈Z）．
8．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1、F2，中心为O，P为双曲线右支上一点，Q为OF2中点，且PQ过△PF1F2的内心，当∠POF2最大时，则双曲线的离心率为$\frac{\sqrt{10}}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网