题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}-{x^2}+3x,x<0\\ ln(x+1),x≥0\end{array}\right.$,若|f(x)|≥ax,则a的取值范围是( )| A. | (-∞,0] | B. | (-∞,1] | C. | [-3,0] | D. | [-3,1] |
分析 ①当x>0时,根据ln(x+1)>0恒成立,求得a≤0.②当x≤0时,可得x2-3x≥ax,求得a的范围.再把这两个a的取值范围取交集,可得答案.
解答 解:当x>0时,根据ln(x+1)>0恒成立,则此时a≤0.
当x≤0时,根据-x2+3x的取值为(-∞,0],|f(x)|=x2-3x≥ax,
x=0时 左边=右边,a取任意值.
x<0时,有a≥x-3,即a≥-3.
综上可得,a的取值为[-3,0],
故选:C.
点评 本题主要考查绝对值不等式的解法,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
10.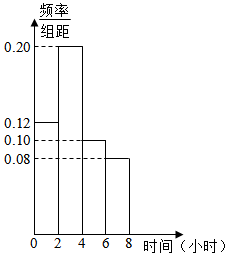 研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是( )
研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是( )
 研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是( )
研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是( )| A. | 1.78小时 | B. | 2.24小时 | C. | 3.56小时 | D. | 4.32小时 |
14.在△ABC中,角A,B,C的对边分别为a,b,c,若$sinA=2sinB,cosC=-\frac{1}{4}$,则$\frac{c}{a}$=( )
| A. | $\sqrt{6}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
11.将函数y=cos(2x+$\frac{π}{3}$)的图象向左平移$\frac{π}{6}$个单位,得到函数y=f(x)的图象,则下列说法正确的是( )
| A. | f(x)是偶函数 | B. | f(x)周期为$\frac{π}{2}$ | ||
| C. | f(x)图象关于x=$\frac{π}{6}$对称 | D. | f(x)图象关于(-$\frac{π}{6}$,0)对称 |
12.已知复数z足zi=-1+i,则z等于( )
| A. | -1-i | B. | 1-i | C. | -1+i | D. | 1+i |