题目内容

函数f（x）=log2（2x）的图象大致是（　　）
A、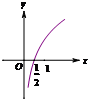
B、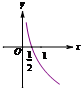
C、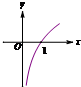
D、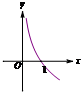
考点：函数的图象
专题：函数的性质及应用
分析：先把函数等价变形，函数f（x）=log2（2x）=log22+log2x=1+log2x，此函数可由对数函数y=log2x向上平移1个单位得到，结合4个选项选出答案．
解答： 解：函数f（x）=log2（2x）=log22+log2x=1+log2x，
故此函数可由对数函数y=log2x向上平移1个单位得到，
选项C的图象为函数y=log2x的图象，平移后为选项A的图象，其它不符合，
故选：A．
点评：本题主要考查对数函数的图象及函数的平移知识，常见函数的图象应熟练掌握．
练习册系列答案
相关题目
下列式子正确的是（　　）
A、（
a
-
b
）2=
a
2-
b
2
B、
a
|
a
|=
a
2
C、|
a
-
b
|≥|
a
|-|
b
|
D、
a
-（
b
-
c
）=（
a
-
b
）-
c
若向量
a
，
b
满足：|
a
|=
2
，|
b
|=2且（
a
-
b
）⊥
a
，则
a
与
b
的夹角是（　　）
A、
π
6
B、
π
4
C、
π
3
D、
5
12
π
若0＞m＞n，则下列结论正确的是（　　）
A、2m＜2n
B、m+
1
m
＞n+
1
n
C、log
1
2
(-m)＜log
1
2
(-n)
D、m2＜n2
∫
3
-3
（x2-2sinx）dx=
 
．
平面内给定三个向量
a
=（3，2），
b
=（-1，2），
c
=（4，1），若
a
=m
b
+n
c
，则n-m=
 
．
已知n∈N*，数列{dn}满足dn=
3+(-1)n
2
，数列{an}满足an=d1+d2+d3+…+d2n；数列{bn}为公比大于1的等比数列，且b2，b4为方程x2-20x+64=0的两个不相等的实根．
（Ⅰ）求数列{an}和数列{bn}的通项公式；
（Ⅱ）将数列{bn}中的第a1项，第a2项，第a3项，…，第an项，…删去后剩余的项按从小到大的顺序排成新数列{cn}，求数列{cn}的前2015项和．
数列{an}满足a1=2，an=
an+1-1
an+1+1
，其前n项积Tn，则T2015=（　　）
A、1B、-6C、2D、3
已知圆C的圆心在直线y=x-1上，且A（2，0），B（
9
5
，
3
5
）在圆C上．
（1）求圆C的方程；
（2）若圆M：x2+（y-2
2
）2=r2（r＞0）与圆C相切．求直线y=
7
x截圆M所得弦长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网